Apriori 关联规则学习方法
介绍
关联规则学习是一种在大型数据库中发现变量之间的有趣关系的方法。它的目的是利用一些有趣的量度来识别数据库中发现的强规则。关联规则被广泛应用于购物篮分析、网络用法挖掘、入侵检测、连续生产及生物信息学。
知识点
- 关联规则
- 频繁项集
- 支持度
- 置信度
- 示例购物数据
- 关联规则任务
- Apriori 算法
- 关联规则实战
关联规则
关联规则(英语:Association Rule)是数据挖掘中的一种发现变量之间有趣关系的手段和方法,它主要的用途是发现数据之间的关联性和强规则。简单来讲,当某类别数据或某个模式在数据集中出行的频率增大时,自然大家都会认为其肯能会更为常见或重要。那么,如果发现两个或多个类别数据同时出现,自然就可以认为其相互之间存在联系或规则。
关联规则最典型的例子就是用于购物篮分析。一些商家发现当顾客购买商品 A 的时候,很容易同时购买商品 B,于是就可以因此调整商品的摆放位置或变换定价策略。这里有一个关于 啤酒和尿布 的故事:大意是一家大型超市的销售团队发现,每周五下午购买尿布的年轻美国男性也有购买啤酒的倾向,于是每周五都会将一个尿布货架放置在啤酒货架旁边,结果是二者的销量都有所上升。
上面这个例子几乎每一篇讲「关联分析」的文章都会用到。那么,销售团队是怎样发现这个购买规律的呢?其中就包含了「关联分析」的使用。
在正式介绍关联分析涉及到的相关算法前,我们先搞清楚关联分析过程中常接触到的几个概念。
频繁项集
首先,我们了解项集的概念。假设有一个集合 $I$ 如下:
那么,我们称其中的 $i_1, i_2, ..., i_m$ 为集合的项 Item,而 $I$ 自然被称之为项 Item 的集合。
此时,若集合 $S$ 满足 $S={i|i∈I}$,则 $S$ 被称之为 $I$ 的项集 Itemset。其中,包含 $k$ 个项的项集称为 $k$-项集。
举个例子,当我们在超市购物时,如果我们的购物车中包含有许多品类的货品,购物车就可以被看作是集合 $I$。此时,如果购物车中有啤酒和尿布,那么啤酒和尿布就可以组成集合 $I$ 的项集 $S$。如果我们把整个超市一天的全部账单看作是集合 $I$,那么单个购物车中出现的商品集合就可以被看作是项集 $S$。
而频繁项集则表明一个项集出现很「频繁」。从直观的角度理解,你应该会认为对频繁项集的挖掘是有意义的,就例如上面的「啤酒和尿布」,因为它们出现的频率很高,最终我们就可以通过调整销售规则来获益。
但是,如何去衡量频繁项集中的「频繁」呢?达到怎样的程度才能被称之为「频繁」呢?
在关联规则中,我们通常会使用 $X → Y$ 这样的表达式。其中,$X$ 和 $Y$ 是不相交项集,即 $X\cap Y=∅$。而关联规则的强度可以用它的支持度(support)和置信度(confidence)度量。
支持度
支持度 support 用来衡量事件发生的频率。$support(X \to Y)$ 则表示项集 ${X,Y}$ 在总项集 $I$ 里出现的频率,记作:
如果依旧拿超市购物举例。上式中,$support(X \to Y)$ 表示同时包含商品 $X$ 和 $Y$ 的购物车占总购物车数量的百分比。例如,$X$ 代表啤酒,$Y$ 代表尿布。那么,我们统计同时包含啤酒和尿布的购物车数量,将结果除以购物车总数,得到该项集的支持度。如果项集的支持度超过预先设定的最小支持阈值,则认为该项集可能是有用的,也就被称之为「频繁项集」。
置信度
置信度 confidence 用来表示在 $X$ 出现情况下,出现 $Y$ 的可能性,其公式为:
那么,$confidence(X \to Y)$ 表示在 $X$ 出现的情况下,$Y$ 出现的概率。即购物车中出现啤酒时,尿布出现的概率。置信度是同时包含 $X$ 和 $Y$ 的购物车的百分比除以只包含 $X$ 的购物车百分比。
简而言之,支持度表示 $X$ 和 $Y$ 同时出现的概率,而置信度表示在 $X$ 出现的情况下,$Y$ 也出现的概率,即条件概率 $P(Y|X)$。
有了支持度和置信度之后,频繁项集就可以被扩展为关联规则了。也就是说如果我们有一条规则如下:
- $support(啤酒→尿布) = 10\%$
- $confidence(啤酒→尿布) = 60\%$
即表示,在超市的销售记录中。有 $10\%$ 的顾客的购物车中出现了啤酒和尿布的组合。同时,购买啤酒的顾客有 $60\%$ 的几率会购买尿布。关联规则的左侧是确定项,称作先导。右侧是结果项,称作后继。
示例购物数据
为了帮助大家熟悉关联规则中出现的相关概念,接下来我们设定一组示例数据,并尝试计算几条规则的支持度和置信度。
| 购物车 | 商品 | 商品 | 商品 | 商品 | 商品 |
|---|---|---|---|---|---|
| 购物车 A | 牛奶 | 咖啡 | - | - | - |
| 购物车 B | 可乐 | 咖啡 | 牛奶 | 啤酒 | - |
| 购物车 C | 啤酒 | 尿布 | 牛奶 | - | - |
| 购物车 D | 咖啡 | 牛奶 | 香蕉 | 雪碧 | 啤酒 |
| 购物车 E | 啤酒 | 尿布 | 咖啡 | - | - |
上面的表格中,出现了 5 个购物车的记录。接下来,我们指定规则为:${牛奶,咖啡} \rightarrow {啤酒}$
首先,项集 ${牛奶,咖啡,啤酒}$ 的支持度计数为 2,总计数为 5,所以:
由于项集 ${牛奶,咖啡}$ 的支持度计数是 3,因此该规则的置信度为:
也就是说,有 $40\%$ 的顾客同时买了牛奶、咖啡和啤酒。而买牛奶和咖啡的顾客中,买啤酒的概率为 $67\%$。
对于一条规则的支持度和置信度而言。支持度的意义在于帮助我们确定这条规则是否有必要被关注。也就是说,我们通常会直接忽略掉支持度低的规则。于此同时,置信度的意义在于帮助我们确定规则的可靠性,是否有足够的数据表明该条规则是大概率存在的。
关联规则任务
上面的内容中,我们学习了关联规则的表示方法,以及单条规则所涉及到的 3 个与之相关的概念。事实上,关联规则挖掘就是从众多的项集中去发现支持度和置信度大于我们所设定阈值的规则。
上面这句话听起来简单,但可以想象的是,实现起来一点都不容易。因为,真实情况下面对的数据集可远复杂于我们上面呈现的示例数据。那么,不同项集的组合,规则的组合数量会变得非常庞大。更具体地说,从包含 $n$ 个项的数据集中提取出的可能规则总数为(排列组合问题):
例如,对于上面包含 5 个不同商品的数据集而言,可以组合 $3^5 - 2^{5+1}+1 = 180$ 条不同的规则。其项集 ${牛奶,咖啡,啤酒}$ 就可以组合为 $3^3 - 2^{3+1}+1 = 12$ 条不同的规则:
虽然项集 ${牛奶,咖啡,啤酒}$ 可以产生上面的 12 条规则,但后面的 6 条规则也可以被看作是其子集 ${牛奶,咖啡}$ ,${牛奶,啤酒}$ ,${咖啡,啤酒}$ 产生。对于这 12 条规则而言,前面 6 条支持度相同,后面 6 条拥有相同项集的两两之间的支持度相同。由于支持度的计算方法只有项集在数据集中出现的频率有关。那么,如果项集 ${牛奶,咖啡,啤酒}$ 是非频繁项集,就可以直接剪掉前 6 条规则而不计算其置信度,从而节省计算开销。
也就是说,关联规则挖掘就被分解成 2 个子任务:
- 发现频繁项集:发现满足最小支持度阈值的所有项集,也就是所说的「频繁项集」。
- 计算关联规则:从发现的频繁项集中提取所有高置信度的规则,作为关联规则挖掘结果。
Apriori 算法
我们通常使用「格结构」来枚举数据集可能存在的项集。如下方格结构图所示,牛奶,咖啡,啤酒组成的数据集可能产生的项集如下:
如上所说,由牛奶,咖啡,啤酒组成的数据集中,可能产生 7 个候选项集(包含单个项组成的项集)。推广到一般情况,则包含 $n$ 个项的数据集,可能产生 $2^n - 1$ 个候选项集。
那么,当我们想从候选项集中找出频繁项集时。笨办法是通过计算每个候选项集的支持度计数,但随着 $n$ 增加,计算开销可想而知。于是,就有了使用 Apriori 先验原理来减少候选项集数量的方法。
Apriori 算法最先于 1994 年在论文 Fast algorithms for mining association rules in large databases 中首次出现,它也是关联规则挖掘中最常用的方法。
Apriori 先验原理说起来非常简单,它主要是告诉我们 2 条定理,即:
- 定理 1:如果一个项集是频繁项集,那么其所有的子集也一定是频繁项集。
- 定理 2:如果一个项集是非频繁项集,那么其所有的超集也一定是非频繁项集。
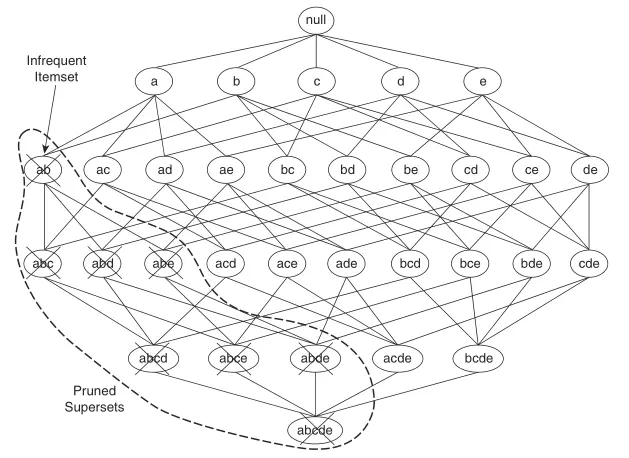
下图呈现了一个比上面例子更大的候选项集格结构图。
基于先验原理,如果我们发现 ${a, b}$ 是非频繁项集,则整个包含 ${a, b}$ 的超集子图都可以被剪枝。于是使用 Apriori 算法产生频繁项集算法过程如下:
首先,令 $F_k$ 表示频繁 $k$ 项集的集合,$C_k$ 表示候选 $k$ 项集的集合:
- 算法一次扫描整个数据集,计算每个项的支持度,并得到频繁 1 项集的集合 $F_1$。
- 然后,算法使用频繁 $k-1$ 项集产生候选 $k$ 项集,可以使用 $F_{k-1} \times F_{k-1}$ 或 $F_{k-1} \times F_{1}$ 方法。
- 算法再次扫描数据集对候选项集完成支持度计数,并使用子集函数确定在 $C_k$ 中的全部候选 $k$ 项集。
- 计算候选项集的支持度,并删去支持度小于预先设定阈值的候选项集。
- 当没有频繁项集产生,即 $F_k = \emptyset$ 时,算法结束。
产生完频繁项集,就可以从给定的频繁项集中提取关联规则。一般情况下,每个频繁 $k$ 项集能够产生 $2^k−2$ 个关联规则。产生出来的规则需要基于置信度剪枝,以满足提前设定的置信度阈值。
这里,我们又要给出一条关于置信度的定理。假设项集 $Y$ 可以被划分为两个非空子集 $X$ 和 $Y-X$,那么:
- 如果规则 $X → Y - X$ 不满足置信度阈值,则规则 $X' → Y - X'$ 一定不满足置信度阈值。其中 $X'$ 是 $X$ 子集。
Apriori 算法使用逐层方法来产生关联规则,其中每层对应于规则后件中的项数。初始时,提取规则后半部分只含一个项的所有高置信度规则;然后,使用这些规则来产生新的候选规则。
关联规则实战
虽然关联规则说到底就是找频繁项集和计算置信度,听起来很简单,但是想要计算变得高效还是比较麻烦的过程。就拿 Apriori 算法举例,Python 完整的实现大约需要 200+ 行代码。所以,这篇文章中就不再动手实现。
接下来,我们使用关联规则挖掘来对一个示例销售数据集进行实战练习。这里,我们使用到了 mlxtend 机器学习算法库提供的 Apriori 算法 API。该 API 完全按照 Fast algorithms for mining association rules in large databases 论文进行实现。
首先,这里给出一个示例购物数据集,二维列表中的每一个列表代表单个购物车中商品名称。
dataset = [['牛奶', '洋葱', '牛肉', '芸豆', '鸡蛋', '酸奶'],
['玉米', '洋葱', '洋葱', '芸豆', '豆腐', '鸡蛋'],
['牛奶', '香蕉', '玉米', '芸豆', '酸奶'],
['芸豆', '玉米', '香蕉', '牛奶', '鸡蛋'],
['香蕉', '牛奶', '鸡蛋', '酸奶'],
['牛奶', '苹果', '芸豆', '鸡蛋']]
dataset
我们尝试通过 Apriori 算法生成频繁项集。这里先通过 mlxtend.preprocessing.TransactionEncoder 将列表数据转换为 Apriori 算法 API 可用的格式。mlxtend.preprocessing.TransactionEncoder 类似于独热编码,可以提取数据集中的不重复项,并将每个购物车数据转换为等长度的布尔值表示。mlxtend 提供的 API 使用方法和 scikit-learn 相似。
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
te = TransactionEncoder() # 定义模型
te_ary = te.fit_transform(dataset) # 转换数据集
te_ary
最终,购物车数据集表示如下:
df = pd.DataFrame(te_ary, columns=te.columns_) # 将数组处理为 DataFrame
df
接下来,我们就可以使用 mlxtend.frequent_patterns.apriori API 来生成频繁项集。根据前面的学习内容可知,生成频繁项集时需要指定最小支持度阈值,满足阈值的候选集将被定为频繁项集。
from mlxtend.frequent_patterns import apriori
apriori(df, min_support=0.5) # 最小支持度为 0.5
默认情况下,apriori 返回项的是列索引,这是为了方便生成关联规则时使用。为了更好的可读性,这里可以设置 use_colnames=True 参数将索引转换为相应的项目名称:
apriori(df, min_support=0.5, use_colnames=True)
此时,如果你只想查看至少包含两个项的频繁项集,就可以通过 Pandas 选择完成:
frequent_itemsets = apriori(df, min_support=0.5, use_colnames=True)
frequent_itemsets[frequent_itemsets.itemsets.apply(lambda x: len(x)) >= 2] # 选择长度 >=2 的频繁项集
有了频繁项集,接下来我们就可以使用 mlxtend.frequent_patterns.association_rules 来生成关联规则了。此时,需要指定最小置信度阈值。
from mlxtend.frequent_patterns import association_rules
association_rules(frequent_itemsets, metric="confidence", min_threshold=0.6) # 置信度阈值为 0.6
association_rules(frequent_itemsets, metric="confidence", min_threshold=0.8) # 置信度阈值为 0.8
mlxtend 使用了 DataFrame 而不是 → 来展示关联规则。其中:
antecedents:规则先导项consequents:规则后继项antecedent support:规则先导项支持度consequent support:规则后继项支持度support:规则支持度confidence:规则置信度lift:规则提升度,表示含有先导项条件下同时含有后继项的概率,与后继项总体发生的概率之比。leverage:规则杠杆率,表示当先导项与后继项独立分布时,先导项与后继项一起出现的次数比预期多多少。conviction:规则确信度,与提升度类似,但用差值表示。
前面的内容中,我们并没有介绍提升度、杠杆率和确信度的概念。这其实是关联规则中用于评估的补充规则,并不必须。
提升度的计算公式如下:
其中,当先导项与后继项独立分布时,值为 1,提升度越大,表示先导项与后继项的关联性越强。
杠杆率的计算公式如下:
其中,当先导项与后继项独立分布时,值为 0。杠杆率越大,表示先导项与后继项的关联性越强。
确信度的计算公式如下:
确信度值越大,则先导项与后继项的关联性越强。
小结
这篇文章中,我们介绍了关联规则学习方法,重点理解了其中涉及到的几个概念,最后使用 mlxtend 机器学习库对 Apriori 算法进行了实战练习。实验并没有从原理上对算法进行纯 Python 实现,因为涉及到的算法原理实在有些麻烦。当然如果你有兴趣的话,推荐几个 Apriori 算法开源项目查阅源代码学习,它们分别是:
系列文章
- 常见数据文件存储和读取
- 数据可视化及初步探索
- 数据预处理之数据清洗
- 数据预处理之数据集成
- 数据预处理之数据转换
- 数据预处理之数据规约
- Apriori 关联规则学习方法
- 时间序列数据分析处理
- 时间序列数据建模分析
- Prophet 因素分解工具实践
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️