数据分析：数据可视化及初步探索
介绍
数据可视化是数据分析过程中必不可少的手段，它几乎贯穿于整个数据分析全程。这篇文章将介绍数据可视化中静态图形的绘制，并学习 Python 中两个十分出色的数据可视化模块 Matplotlib 和 Seaborn。最后，你会利用所学的可视化知识，对经典数据分析 iris 数据集进行初步的数据探索。
知识点
- 可视化与数据挖掘的步骤
- Matplotlib 绘制图形
- Matplotlib 添加图形属性
- 等高线的绘制
- 泊松分布和正态分布的绘制
- Seaborn 密度估计图的绘制
- 单变量变量图的绘制
- 热力图的绘制
可视化与数据挖掘
在数据挖掘过程中，可视化是一项重要的工作。它一般开始于拿到数据之后，直到得到完整的数据分析结论。也就是说，数据可视化贯穿于整个数据分析过程之中，而不是在某个阶段特定的一项操作。
- 拿到数据之后：数据可视化可以让我们快速了解数据及分布。
- 数据预处理中：数据可视化能让我们发现数据规律或异常，实施相应预处理手段。
- 数据建模时：数据可视化能追逐模型指标变化。
- 数据分析报告：数据可视化是分析报告必不可少的内容，一图抵千言。
数据可视化，简单来讲就是画图，但是画图却没有想象中的那么简单。数据可视化中往往会涉及到各种类型、各种样式、静态或动态等不同图形的绘制。除此之外，数据可视化的难点在于「不同情形下的不同可视化手段」，也就是什么情况下该画哪种图形。
这篇文章中，我们重点了解数据可视化的基本方法，以及在拿到数据之后，探索数据集时的常见操作。关于更多的可视化内容，我们将会在之后的实验中慢慢抛出。
Matplotlib 模块介绍
在日常的工作和学习过程中，我们都会遇到需要针对数据进行绘图的时候。谈起数据绘图，你应该最先想到的是 Excel。Excel 操作起来相对简单，提供的图形样式也可以满足大部分人日常绘图的需要。
但是，如果你处于工程、数据科学相关专业领域，使用 Excel 绘图就显得捉襟见肘了。首先，Excel 默认 提供的图形样式有限，其次是自定义程度不高。
很多时候，我们会使用到 Matlab 提供的绘图模块，又或者使用 Origin 进行绘图。这些软件固然都很不错，但均为商业软件，使用时需要获得授权。
Matplotlib 是支持 Python 语言的开源绘图库，因为其支持丰富的绘图类型、简单的绘图方式以及完善的接口文档，深受 Python 工程师、科研学者、数据工程师等各类人士的喜欢。Matplotlib 拥有着十分活跃的社区以及稳定的版本迭代，当我们使用 Python 进行数据分析并执行可视化时，Matplotlib 无疑是得心应手的工具之一。
Matplotlib 绘制线型图
折线图是在序列中表达数据变量的统计图表，通常用于发现数据集中的趋势，其暗示数据的变化往往包含时间或其他特定因素。
下面我们用 Matplotlib 来简单绘制一下折线图：
# 导入 Matplotlib 绘图模块
from matplotlib import pyplot as plt
%matplotlib inline
y = [1, 2, 3, 2, 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
plt.plot(y)
第二行代码是从 Matplotlib 中导入了 pyplot 绘图模块，并将其简称为 plt。pyplot 模块是 Matplotlib 最核心的模块，几乎所有样式的 2D 图形都是经过该模块绘制出来的，这里简称为 plt 是约定俗成的。
plt.plot() 是 pyplot 模块下面的直线绘制（折线类）方法类。代码中，它取出 x 数据集中的内容，将其按大小打印到图中，并以直线连接每个点。
通常，plot() 接受两个参数。一个代表横坐标的数值，另一个代表纵坐标的数值。但是，当你只传入一个参数 y 的时候，它会默认代表纵坐标的值，而横坐标的值会从 0 到 n-1，n 为 y 数据长度。
# 运行下面代码，输出一致的图形
x = [i for i in range(len(y))] # 生成与 y 等长度 x
plt.plot(x, y)
Matplotlib 绘图时，当点非常密集时，折线就会变成光滑的曲线。例如，我们绘制正弦函数的曲线。
import numpy as np
# 在 -2PI 和 2PI 之间等间距生成 1000 个值，也就是 X 坐标
X = np.linspace(-2*np.pi, 2*np.pi, 1000)
# 计算 y 坐标
y = np.sin(X)
plt.plot(X, y)
你还可以通过改变产生数据的数量来观察图像的变化。
X = np.linspace(-5*np.pi, 5*np.pi, 10)
y = np.sin(X)
plt.plot(X, y)
上面从同一个函数关系中产生数据集，但是绘制的图像却相差甚远。原因是，第二个数据集中数量点太少，获得的信息不足描述 $y$ 和 $x$ 之间的关系。这现象反映一个这样的道理，当你拥有更大的数据集，你能更容易地通过可视化手段发现藏在数据背后的规律。
Matplotlib 添加图形属性
当你学会线型图绘制之后，可能想到改变图形的属性。例如，更改图形的尺寸、添加图例等。Matplotlib 提供的面向对象 API 使用起来非常简单，但是下面不再直接使用 plt.plot，而是定义一个绘图对象 fig, axes = plt.subplots()。
# 生成示例数据
x = np.linspace(0, 10, 20)
y = x * x + 2
fig, axes = plt.subplots()
axes.plot(x, y, 'r')
上面的绘图代码中，你可能会对 figure 和 axes 产生疑问。Matplotlib 的 API 设计的非常符合常理，在这里，figure 相当于绘画用的画板，而 axes 则相当于铺在画板上的画布。我们将图像绘制在画布上，于是就有了 plot，set_xlabel 等操作。
那么，如果想要调节画布尺寸和显示大小，只需要向 plt.subplots 中添加参数即可。
# 通过 figsize 调节尺寸, dpi 调节显示精度
fig, axes = plt.subplots(figsize=(16, 9), dpi=50)
axes.plot(x, y, 'r')
当然，你还可能需要绘制图名称、坐标轴名称、图例等信息。
# 绘制包含图标题、坐标轴标题以及图例的图形
fig, axes = plt.subplots()
axes.set_xlabel('x label')
axes.set_ylabel('y label')
axes.set_title('title')
axes.plot(x, x**2)
axes.plot(x, x**3)
axes.legend(["y = x**2", "y = x**3"], loc=2)
图例中的 loc 参数标记图例位置，1，2，3，4 依次代表：右上角、左上角、左下角，右下角；0 代表自适应。
同样，我们可以绘制子图。向 plt.subplots 中添加参数 nrows 和 ncols 参数即可。
fig, axes = plt.subplots(nrows=1, ncols=2) # 子图为 1 行，2 列
axes[0].plot(x, y, 'r')
axes[1].plot(x, y, 'b')
Matplotlib 其他常见图形
除了线型图，Matplotlib 还支持绘制散点图、柱状图等其他常见图形。例如：
# 绘制散点图、梯步图、条形图、面积图
n = np.array([0, 1, 2, 3, 4, 5])
fig, axes = plt.subplots(1, 4, figsize=(16, 5))
axes[0].scatter(x, x + 0.25*np.random.randn(len(x)))
axes[0].set_title("scatter")
axes[1].step(n, n**2, lw=2)
axes[1].set_title("step")
axes[2].bar(n, n**2, align="center", width=0.5, alpha=0.5)
axes[2].set_title("bar")
axes[3].fill_between(x, x**2, x**3, color="green", alpha=0.5)
axes[3].set_title("fill_between")
绘制直方图
n = np.random.randn(100000)
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].hist(n)
axes[0].set_title("Default histogram")
axes[0].set_xlim((min(n), max(n)))
axes[1].hist(n, cumulative=True, bins=50)
axes[1].set_title("Cumulative detailed histogram")
axes[1].set_xlim((min(n), max(n)))
绘制雷达图：
fig = plt.figure(figsize=(6, 6))
ax = fig.add_axes([0.0, 0.0, .6, .6], polar=True)
t = np.linspace(0, 2 * np.pi, 100)
ax.plot(t, t, color='blue', lw=3)
Matplotlib 绘制复杂图形
Matplotlib 可以绘制出很多复杂图形，当然这需要根据实际需求确定，绘图的代码也会复杂很多。例如，我们这里尝试绘制一个等高线图。
alpha = 0.7
phi_ext = 2 * np.pi * 0.5
def flux_qubit_potential(phi_m, phi_p):
return 2 + alpha - 2 * np.cos(phi_p) * np.cos(phi_m) - alpha * np.cos(phi_ext - 2*phi_p)
phi_m = np.linspace(0, 2*np.pi, 100)
phi_p = np.linspace(0, 2*np.pi, 100)
X, Y = np.meshgrid(phi_p, phi_m)
Z = flux_qubit_potential(X, Y).T
fig, ax = plt.subplots()
cnt = ax.contour(Z, cmap=plt.cm.RdBu, vmin=abs(Z).min(),
vmax=abs(Z).max(), extent=[0, 1, 0, 1])
Matplotlib 绘制风格图形
xkcd 是一个非常有趣的漫画网站，其作品大多充斥着浪漫、讽刺、数学等元素。
Matplotlib 官方提供了模仿 xkcd 漫画风格的绘图样式，你可以通过 plt.xkcd() 来绘制 xkcd 风格的图像。
with plt.xkcd():
plt.hist(np.sin(np.linspace(0, 10)))
plt.title('Sample Data')
Seaborn 模块介绍
Matplotlib 应该是基于 Python 语言最优秀的绘图库了，但是它也有一个十分令人头疼的问题，那就是太过于复杂了。3000 多页的官方文档，上千个方法以及数万个参数，属于典型的你可以用它做任何事，但又无从下手。
尤其是，当你像通过 Matplotlib 调出非常漂亮的效果时，往往会伤透脑筋，非常麻烦。
Seaborn 基于 Matplotlib 核心库进行了更高级的 API 封装，可以让你轻松地画出更漂亮的图形。而 Seaborn 的漂亮主要体现在配色更加舒服、以及图形元素的样式更加细腻。
列举一下 Seaborn 的几个特点：
-
内置数个经过优化的样式效果。
-
增加调色板工具，可以很方便地为数据搭配颜色。
-
单变量和双变量分布绘图更为简单，可用于对数据子集相互比较。
-
对独立变量和相关变量进行回归拟合和可视化更加便捷。
-
对数据矩阵进行可视化，并使用聚类算法进行分析。
-
基于时间序列的绘制和统计功能，更加灵活的不确定度估计。
-
基于网格绘制出更加复杂的图像集合。
除此之外， Seaborn 对 Matplotlib 和 Pandas 的数据结构高度兼容，非常适合作为数据挖掘过程中的可视化工具。
使用 Seaborn 优化 Matplotlib 图形
我们可以通过 Seaborn 对 Matplotlib 绘图完成样式快速优化。以前面的折线图代码为例，在 plt.plot(y) 这行代码前添加上sns.set(style='xx')，指定一个预设样式，能让画出来的图形更加精美。
style 有 5 个参数可选：
darkgrid黑色网格whitegrid白色网格white白色背景ticks加上刻度的白色背景
import seaborn as sns
y = [1, 2, 3, 2, 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
# 将画图风格设置为 darkgrid
sns.set(style='darkgrid')
plt.plot(y)
plt.show()
可以发现，相比于 Matplotlib 默认的纯白色背景，Seaborn 默认的浅灰色网格背景看起来的确要细腻舒适一些。而柱状图的色调、坐标轴的字体大小也都有一些变化。Seaborn 支持的预设样式有 darkgrid, whitegrid, dark, white, ticks，关于它们的效果，你可以亲自动手试一试
使用 Seaborn 绘制图形
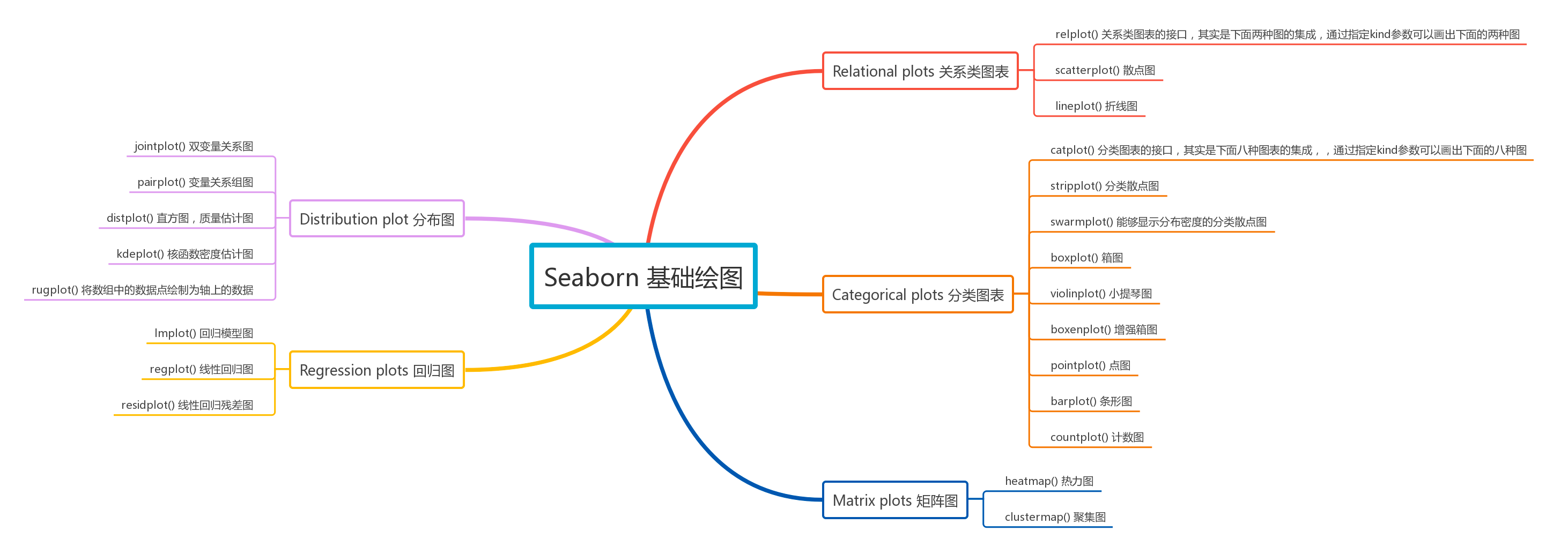
Seaborn 支持常见的五类不同样式的图形绘制，你可以通过下方的思维导图了解。
接下来，我们使用 Seaborn API 来绘制常见的图形。
直方图
我们可以通过 seaborn.distplot 绘制单变量的直方图。下面，我们通过构造两个不同分布的数据集，并以画图展示。
seaborn.distplot(a, bins=None, hist=True, kde=True, rug=False, fit=None, hist_kws=None, kde_kws=None, rug_kws=None, fit_kws=None, color=None, vertical=False, norm_hist=False, axlabel=None, label=None, ax=None)
首先，我们来构造 正态分布 的数据集。
x = np.random.normal(size=500)
sns.distplot(x)
你还可以根据 泊松分布 公式，构造参数为 1 ， 大小为 1000 的泊松分布数据集，并画出其分布图。
poisson = np.random.poisson(1, 300)
sns.distplot(poisson)
你可以发现，seaborn.distplot 不仅绘制了直方图，还自动添加了变化趋势曲线。
组合图
seaborn.jointplot 可以用来绘制单变量和双变量的组合图。
seaborn.jointplot(x, y, data=None, kind='scatter', stat_func=None, color=None, height=6, ratio=5, space=0.2, dropna=True, xlim=None, ylim=None, joint_kws=None, marginal_kws=None, annot_kws=None, **kwargs)
下面我们利用多元正态分布的公式和 NumPy 提供的函数来构造数据集，然后用 joinplot() 可视化两个变量之间的关系。
# 根据公式，构造数据集
mean = [0, 0]
cov = [[1, 0], [0, 10]] # 协方差矩阵
x, y = np.random.multivariate_normal(mean, cov, 300).T
# 画出 x, y 的联合分布图
sns.jointplot(x=x, y=y)
核密度估计图
核密度估计是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。
seaborn.kdeplot(data, data2=None, shade=False, vertical=False, kernel='gau', bw='scott', gridsize=100, cut=3, clip=None, legend=True, cumulative=False, shade_lowest=True, cbar=False, cbar_ax=None, cbar_kws=None, ax=None, **kwargs)
data: 一维数组shade: 是否保留阴影面积cut: 数轴极限数值的多少cumulative: 是否绘制累积分布
kdeplot 主要是用于绘制单变量或变量的核密度估计图。先看看单变量的效果。
# shade 参数表示是否需要曲线阴影面积
sns.kdeplot(x, shade=True)
我们可以将三个变量的密度图在同一个图画出来，以便比较它们之间分布的差别。
sns.kdeplot(x, label='x')
sns.kdeplot(y, label='y')
sns.kdeplot(poisson, label='poisson')
$x$ 和 $ poisson $ 变量的联合密度图：
# x 和 poisson 变量的联合密度图
sns.jointplot(x=x, y=poisson, kind='kde')
$x$ 和 $y$ 的联合概率密度图：
sns.jointplot(x=x, y=y, kind='kde')
计数图
计数图 countplot 是一类可以对数据集分类的直方图，使用图形显示每个分类中的数量，同时也可以比较类别间数量差。
seaborn.countplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, orient=None, color=None, palette=None, saturation=0.75, dodge=True, ax=None, **kwargs)
x, y: 变量的名字hue: 分类变量的名字data: 数据集，DataFrame类型
下面，我们利用一个练习数据集 planets 中的 year 特征，分类计算每年的数据是多少。
planets = sns.load_dataset("planets")
planets.head(5)
为了显示效果，我们选取了 2005 年至今的年份计数，看数据集相应年份有多少数据点。
count_year = sns.countplot(x="year", data=planets[planets['year'] > 2005])
Seaborn 绘制子图
你可能会想使用 Seaborn 绘制子图，那么应该怎么做了。实际上，因为 Seaborn 来源于 Matplotlib，它们之间的界限非常模糊，很多都可以关联使用。例如，你可以类比 Matplotlib 绘制子图的方法来绘制 Seaborn 子图。
例如，我们把上面的直方图和和密度估计图绘制成横向拼接的子图。
fig, axes = plt.subplots(ncols=2, nrows=1, figsize=(12, 5))
# 使用 ax 参数指定 axes 对象
sns.distplot(x, ax=axes[0])
sns.kdeplot(x, ax=axes[1])
鸢尾花数据集探索
鸢尾花数据集是数据挖掘领域一个非常经典的分类数据集。接下来，我们就以这个数据集为基础，进行可视化探索。
在绘图之前，我们先熟悉一下 iris 鸢尾花数据集。数据集总共 150 行，由 5 列组成。分别代表：萼片长度、萼片宽度、花瓣长度、花瓣宽度、花的类别。其中，前四列均为数值型数据，最后一列花的分类为三种，分别是：Iris Setosa、Iris Versicolour、Iris Virginica。
导入这个数据集很简单，这里我们通过 Seaborn 内置的数据集类直接导入。
iris_data = sns.load_dataset('iris') # 导入 iris_data 数据集
iris_data.head()
单变量探索
单变量探索就是，挖掘每个特征数据本身的规律。例如，自身分布、均值、方差、众数、中位数、百分比等。
iris_data['species'].value_counts()
利用 sns.distplot 查看各个特征自身的分布：
sns.distplot(iris_data['sepal_length'], color='red')
sns.distplot(iris_data['sepal_width'], color='blue')
sns.distplot(iris_data['petal_length'], color='green')
sns.distplot(iris_data['petal_width'], color='black')
从图中可以直观看出，四个特征属性的中位数、众数等、取值范围等统计信息。
多变量探索
我们可以利用散点图、折线图、二维分布图等，探索两两变量之间的关系。下面，以 sepal_length 和 sepal_width 属性为例，探索两个变量的关系。
sns.jointplot(x=iris_data['sepal_length'], y=iris_data['sepal_width'])
你还可以使用 pairplot，画出整个数据集特征的两两关系。
sns.pairplot(iris_data)
这里，我们可以定义一些参数，将图画得更好看一些。
sns.pairplot(iris_data, hue="species", diag_kind="kde")
seaborn.lmplot() 是一个非常有用的方法，它会在绘制二维散点图时，自动完成回归拟合。
sns.lmplot(x='sepal_length', y='sepal_width', hue='species', data=iris_data)
sns.lmplot() 里的 x, y 分别代表横纵坐标的列名。hue= 代表按照 species，即花的类别分类显示，而 data= 自然就是关联到数据集了。
由于 Seaborn 对 Pandas 的 DataFrame 数据格式高度兼容，所以一切变得非常简单。绘制出来的图也自动带有图例，并进行了线型回归拟合，还给出了置信区间。
seaborn.heatmap() 主要是用于绘制热力图，也就类似于色彩矩阵。还记得我们在「数据清洁与预处理」章节中介绍过的皮尔逊相关系数吗？用 seaborn.heatmap() 绘制出来，可比看数据要直观很多。
sns.heatmap(iris_data.corr(), square=True, annot=True) # corr() 函数计算皮尔逊相关系数
小结
本节实验对 Matplotlib 和 Seaborn 的使用进行了学习，掌握了常用图形的绘制方法，已经能满足数据分析过程中的基本需要。除此之外，我们使用 Seaborn 对经典的 iris 数据集进行了探索，对数据的分布有了直观的了解。由于数据可视化充分融入在数据分析中，所以通过一个实验来学习不太现实。不同图形的绘制，以及不同可视化方法的不同用法，将在后续的实验中逐步介绍。