人工神经网络数学推导及 Python 实现
人工神经网络是深度学习的基石,也是机器学习中一种十分重要的算法。与此同时,反向传播算法又是人工神经网络的核心。本文尝试通过数学矩阵完成神经网络的推导,并使用 Python 实现一个简单神经网络的完整结构。
定义神经网络结构
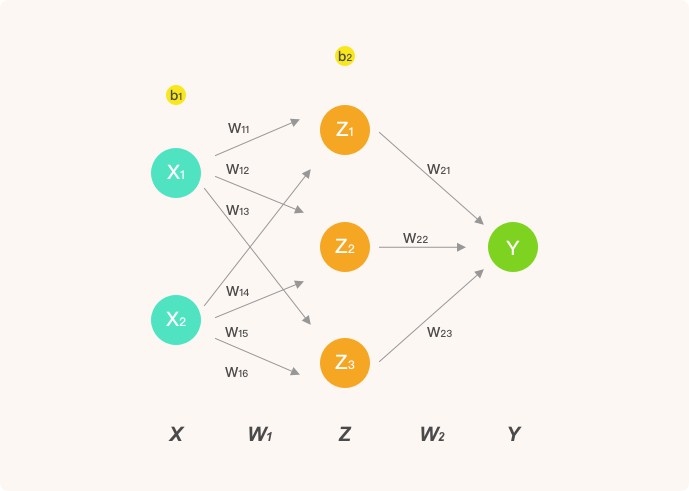
为了让推导过程足够清晰,这里我们只构建包含 1 个隐含层的人工神经网络结构。其中,输入层为 2 个神经元,隐含层为 3 个神经元,并通过输出层实现 2 分类问题的求解。该神经网络的结构如下:
本次实验中,我们使用的激活函数为 $sigmoid$ 函数:
$$\text {sigmoid} ( x ) = \frac { 1 } { 1 + e ^ { - x } }$$
由于下面要使用 $sigmoid$ 函数的导数,所以同样将其导数公式写出来:
$$\Delta sigmoid(x) = \operatorname { sigmoid } ( x ) ( 1 - \operatorname { sigmoid } ( x ) )$$
首先,我们通过 Python 实现公式 (1):
# sigmoid 函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# sigmoid 函数求导
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
前向传播
前向(正向)传播中,每一个神经元的计算流程为:线性变换 → 激活函数 → 输出值。
在此,我们约定:
- $Z$ 表示隐含层输出, $Y$ 则为输出层最终输出。
- $w_{ij}$ 表示从第 $i$ 层的第 $j$ 个权重。
于是,上图中的前向传播的代数计算过程如下。
神经网络的输入 $X$ ,第一层权重 $W_1$ ,第二层权重 $W_2$ 。为了演示方便, $X$ 为单样本,因为是矩阵运算,我们很容易就能扩充为多样本输入。
$$X = \left[ \begin{array} { l l } { x _ { 1 } } & { x _ { 2 } } \end{array} \right] \tag{2a}$$
$$W _ { 1 } = \left[ \begin{array} { l l l } { w _ { 11 } } & { w _ { 12 } } & { w _ { 13 } } \\ { w _ { 14 } } & { w _ { 15 } } & { w _ { 16 } } \end{array} \right] \tag{2b}$$
$$W _ { 2 } = \left[ \begin{array} { c } { w _ { 21 } } \\ { w _ { 22 } } \\ { w _ { 23 } } \end{array} \right] \tag{2c}$$
接下来,计算隐含层神经元输出 $Z$ (线性变换 → 激活函数)。同样,为了使计算过程足够清晰,我们这里将截距项置为 0。
$$Z = \operatorname { sigmoid } \left( X \cdot W _ { 1 } \right) \tag{3a}$$
最后,计算输出层 $Y$ (线性变换 → 激活函数):
$$Y = \operatorname { sigmoid } \left( Z \cdot W _ { 2 } \right) \tag{3b}$$
至此,已经完成了前向传播的推导。
反向传播
接下来,我们使用梯度下降法的方式来优化神经网络的参数。那么首先需要定义损失函数,然后计算损失函数关于神经网络中各层的权重的偏导数(梯度)。
此时,设神经网络的输出值为 $Y$ ,真实值为 $y$ 。然后,定义平方损失函数如下:
$$Y = \operatorname { sigmoid } \left( Z \cdot W _ { 2 } \right) \tag{4}$$
接下来,求解梯度 $\frac{\partial Loss(y, Y)}{\partial{W_2}}$ ,需要使用链式求导法则:
$$\frac { \partial \operatorname { Loss } ( y , Y ) } { \partial W _ { 2 } } = \frac { \partial \operatorname { Loss } ( y , Y ) } { \partial Y } \frac { \partial Y } { \partial W _ { 2 } } \tag{5a}$$
$$\frac { \partial \operatorname { Loss } ( y , Y ) } { \partial W _ { 2 } } = 2 ( Y - y ) * \Delta \operatorname { sigmoid } \left( Z \cdot W _ { 2 } \right) \cdot Z \tag{5b}$$
同理,梯度 $\frac{\partial Loss(y, Y)}{\partial{W_1}}$ 得:
$$\frac { \partial \operatorname { Loss } ( y , Y ) } { \partial W _ { 1 } } = \frac { \partial \operatorname { Loss } ( y , Y ) } { \partial Y } \frac { \partial Y } { \partial Z } \frac { \partial Z } { \partial W _ { 1 } } \tag{6a}$$
$$\frac { \partial \operatorname { Loss } ( y , Y ) } { \partial W _ { 1 } } = 2 ( Y - y ) \Delta \operatorname { sigmoid } \left( Z \cdot W _ { 2 } \right) \cdot W _ { 2 } \Delta \operatorname { sigmoid } \left( X \cdot W _ { 1 } \right) \cdot X \tag{6b}$$
其中, $\frac{\partial Y}{\partial{W_2}}$, $\frac{\partial Y}{\partial{W_1}}$ 分别通过公式 (5) 和 (6) 求得。
然后,就可以设置学习率 $lr$ ,并对 $W_1$ , $W_2$ 进行一次更新了。
$$W _ { 1 } = W _ { 1 } + l r * \frac { \partial \operatorname { Loss } ( y , Y ) } { \partial W _ { 1 } } \tag{7a}$$
$$W _ { 2 } = W _ { 2 } + l r * \frac { \partial \operatorname { Loss } ( y , Y ) } { \partial W _ { 2 } } \tag{7b}$$
以上,我们就实现了单个样本在神经网络中的 1 次前向 → 反向传递,并使用梯度下降完成 1 次权重更新。那么,下面我们完整实现该网络,并对多样本数据集进行学习。
# 示例神经网络完整实现
class NeuralNetwork:
# 初始化参数
def __init__(self, X, y, lr):
self.input_layer = X
self.W1 = np.random.rand(self.input_layer.shape[1], 3) # 注意形状
self.W2 = np.random.rand(3, 1)
self.y = y
self.lr = lr
self.output_layer = np.zeros(self.y.shape)
# 前向传播
def forward(self):
# 实现公式 2,3
self.hidden_layer = sigmoid(np.dot(self.input_layer, self.W1))
self.output_layer = sigmoid(np.dot(self.hidden_layer, self.W2))
# 反向传播
def backward(self):
# 实现公式 5
d_W2 = np.dot(self.hidden_layer.T, (2 * (self.output_layer - self.y) *
sigmoid_derivative(np.dot(self.hidden_layer, self.W2))))
# 实现公式 6
d_W1 = np.dot(self.input_layer.T, (
np.dot(2 * (self.output_layer - self.y) * sigmoid_derivative(
np.dot(self.hidden_layer, self.W2)), self.W2.T) * sigmoid_derivative(
np.dot(self.input_layer, self.W1))))
# 参数更新,实现公式 7
# 因上方是 output_layer - y,此处为 -= 以保证符号一致
self.W1 -= self.lr * d_W1
self.W2 -= self.lr * d_W2
测试网络
接下来,我们使用一组测试数据,并迭代 1000 次:
import numpy as np
from matplotlib import pyplot as plt
# 测试数据
X = np.array([
[1, 0],
[0, 1],
[1, 0],
[1, 1],
])
y = np.array([[0], [1], [0], [1]])
nn = NeuralNetwork(X, y, lr=0.1) # 定义模型
loss_list = [] # 存放损失数值变化
for i in range(1000):
nn.forward() # 前向传播
nn.backward() # 反向传播
loss = np.sum((y - nn.output_layer) ** 2) # 计算平方损失
loss_list.append(loss)
print("final loss:", loss)
plt.plot(loss_list) # 绘制 loss 曲线变化图
测试结果如下:
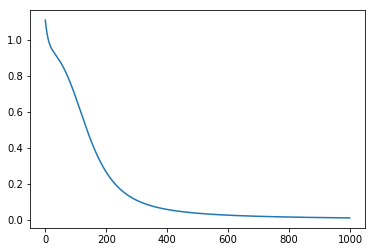
可以看到,损失逐渐减小并接近收敛,本实验重点再于搞清楚 BP 的中间过程,因网络简单,无法直接照搬使用。需要注意的是由于权重是随机初始化,多次运行的结果会不同。
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️