PyTorch 深度学习基础入门
PyTorch 基础语法
PyTorch 是 Facebook 主导开发的,基于 Python 的科学计算包,其主要有以下两个特点:
- 比 NumPy 更灵活,可以使用 GPU 的强大计算能力。
- 开源高效的深度学习研究平台。
接下来,我们了解 PyTorch 的基础概念和语法。
张量
Tensors(张量)与 NumPy 中的 Ndarrays 多维数组类似,但是在 PyTorch 中 Tensors 可以使用 GPU 进行计算。
下面,我们创建一个 $5 \times 3$ 矩阵。使用 torch.empty 可以返回填充了未初始化数据的张量。张量的形状由可变参数大小定义。
import torch
torch.empty(5, 3)
创建一个随机初始化的矩阵:
torch.rand(5, 3)
创建一个 0 填充的矩阵,指定数据类型为 long:
torch.zeros(5, 3, dtype=torch.long)
创建 Tensor 并使用现有数据初始化:
x = torch.tensor([5.5, 3])
x
根据现有张量创建新张量。这些方法将重用输入张量的属性,除非设置新的值进行覆盖。
x = x.new_ones(5, 3, dtype=torch.double) # new_* 方法来创建对象
x
覆盖 dtype,对象的 size 是相同的,只是值和类型发生了变化:
x = torch.randn_like(x, dtype=torch.float)
x
获取张量的 size:
x.size()
小贴士
torch.Size 返回值是 tuple 类型,所以它支持 tuple 类型的所有操作。
操作
针对 Tensor 的操作语法很多,我们先看一下加法运算。其中,加法运算方法就有好多种:
第一种加法运算:
y = torch.rand(5, 3)
x + y
第二种加法运算:
torch.add(x, y)
提供输出 Tensor 作为参数:
result = torch.empty(5, 3)
torch.add(x, y, out=result)
result
替换:
y.add_(x) # 将 x 加到 y
y
小贴士
任何以下划线结尾的操作都会用结果替换原变量。例如:x.copy_(y), x.t_(), 都会改变 x。
你可以使用与 NumPy 索引方式相同的操作来进行对张量的操作:
x[:, 1]
torch.view 可以改变张量的维度和大小:
x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8) # size -1 从其他维度推断
x.size(), y.size(), z.size()
如果张量只有一个元素,使用 .item() 来得到 Python 数据类型的数值:
x = torch.randn(1)
x, x.item()
更多关于 Tensor 操作,包括:转置,索引,切片,数学运算,线性代数,随机数等,可以进一步阅读 官方文档。
NumPy 转换
将 PyTorch 张量转换为 NumPy 数组(反之亦然)是一件轻而易举的事。PyTorch 张量和 NumPy 数组将共享其底层内存位置,改变一个也将改变另一个。
将 PyTorch 张量转换为 NumPy 数组:
a = torch.ones(5)
a
b = a.numpy()
b
了解 NumPy 数组的值如何变化:
a.add_(1)
a, b
NumPy 数组转换成 PyTorch 张量时,可以使用 from_numpy 完成:
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
a, b
所有的 Tensor 类型默认都是基于 CPU, CharTensor 类型不支持到 NumPy 的转换。
CUDA 张量
CUDA 张量是能够在 GPU 设备中运算的张量。使用 .to 方法可以将 Tensor 移动到 GPU 设备中:
# is_available 函数判断是否有 GPU 可以使用
if torch.cuda.is_available():
device = torch.device("cuda") # torch.device 将张量移动到指定的设备中
y = torch.ones_like(x, device=device) # 直接从 GPU 创建张量
x = x.to(device) # 或者直接使用 .to("cuda") 将张量移动到 cuda 中
z = x + y
print(z)
print(z.to("cpu", torch.double)) # .to 也会对变量的类型做更改
小贴士
由于实验未配置 GPU,所以上述代码没有输出结果。如果有 GPU 设备,输出示例如下:
tensor([1.4566], device='cuda:0')
tensor([1.4566], dtype=torch.float64)
Autograd 自动求导
PyTorch 中所有神经网络的核心是 autograd。我们先简单介绍一下这个包,然后训练一个神经网络。
autograd 为张量上的所有操作提供了自动求导。它是一个在运行时定义的框架,这意味着反向传播是根据你的代码来确定如何运行。torch.Tensor 是这个包的核心类。如果设置 .requires_grad 为 True,那么将会追踪所有对于该张量的操作。当完成计算后通过调用 .backward() 会自动计算所有的梯度,这个张量的所有梯度将会自动积累到 .grad 属性。这也就完成了自动求导的过程。
要阻止张量跟踪历史记录,可以调用 .detach() 方法将其与计算历史记录分离。为了防止跟踪历史记录(和使用内存),可以将代码块包装在 with torch.no_grad(): 语句中。这一点在评估模型时特别有用,因为模型可能具有 requires_grad=True 的可训练参数,但是我们并不需要计算梯度。
自动求导中还有另外一个重要的类 Function。Tensor 和 Function 互相连接并生成一个非循环图,其存储了完整的计算历史。
如果需要计算导数,你可以在 Tensor 上调用 .backward()。 如果 Tensor 是一个标量(即它包含一个元素数据)则不需要为 backward() 指定任何参数。但是,如果它有多个元素,你需要指定一个 gradient 参数来匹配张量的形状。
接下来,我们创建一个张量并设置 requires_grad=True 用来追踪他的计算历史:
x = torch.ones(2, 2, requires_grad=True)
x
对张量进行操作,也就是计算过程:
y = x + 2
y
结果 y 已经被计算出来了,所以,grad_fn 已经被自动生成了。
y.grad_fn
然后,再对 y 进行操作:
z = y * y * 3
out = z.mean()
z, out
.requires_grad_( ... ) 可以改变现有张量的 requires_grad 属性。
如果没有指定的话,默认输入的 flag 是 False。
a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)
梯度
上面只是完成了梯度的自动追踪,下面通过反向传播打印对应节点的梯度。因为 out 是一个纯量 Scalar,out.backward() 等于 out.backward(torch.tensor(1))。
out.backward()
打印其梯度:
x.grad
我们可以通过数学公式来验算上面的结果:
$$out = \frac{1}{4}\sum_i z_i$$
$$z_i = 3(x_i+2)^2$$
$$z_i\bigr\rvert_{x_i=1} = 27$$
因此,
$$\frac{\partial out}{\partial x_i} = \frac{3}{2}(x_i+2)$$
$$\frac{\partial out}{\partial x_i}\bigr\rvert_{x_i=1} = \frac{9}{2} = 4.5$$
下面,演示 Autograd 更多的操作:
x = torch.randn(3, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
y
gradients = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(gradients)
x.grad
如果 .requires_grad=True 但是你又不希望进行 Autograd 的计算,那么可以将变量包裹在 with torch.no_grad() 中:
print(x.requires_grad)
print((x ** 2).requires_grad)
with torch.no_grad():
print((x ** 2).requires_grad)
神经网络
PyTorch 中,我们可以使用 torch.nn 来构建神经网络。
上一讲已经讲过了 autograd,torch.nn 依赖 autograd 来定义模型并求导。nn.Module 中包含了构建神经网络所需的各个层和 forward(input) 方法,该方法返回神经网络的输出。
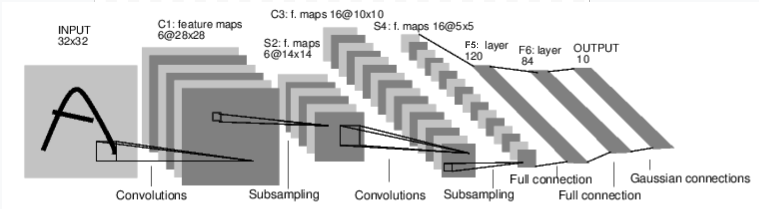
下面给出一个示例网络结构,该网络也是经典的 LeNet。
它是一个简单的前馈神经网络,它接受一个输入,然后一层接着一层地传递,最后输出计算的结果。
神经网络的典型训练过程如下:
- 定义包含可学习参数(权重)的神经网络模型。
- 在数据集上迭代。
- 通过神经网络处理输入。
- 计算损失(输出结果和正确值的差值大小)。
- 将梯度反向传播回网络节点。
- 更新网络的参数,一般可使用梯度下降等最优化方法。
接下来,实验参考上面的过程完成神经网络训练。首先,定义上图示例的神经网络结构:
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:]
num_features = 1
for s in size:
num_features *= s
return num_features
net = Net()
net
模型中必须要定义 forward 函数,backward 函数(用来计算梯度)会被 autograd 自动创建。可以在 forward 函数中使用任何针对 Tensor 的操作。
net.parameters() 返回可被学习的参数(权重)列表和值:
params = list(net.parameters())
print(len(params))
print(params[0].size()) # conv1's .weight
测试随机输入 $32 \times 32$。注意,网络(LeNet)期望的输入大小是 $32 \times 32$,如果使用 MNIST 数据集($28 \times 28$)来训练这个网络,请把图片大小重新调整到 $32 \times 32$。
input = torch.randn(1, 1, 32, 32)
out = net(input)
out
将所有参数的梯度缓存清零,然后进行随机梯度的的反向传播:
net.zero_grad()
out.backward(torch.randn(1, 10))
小贴士
torch.nn 只支持小批量输入。整个 torch.nn
包都只支持小批量样本,而不支持单个样本。例如,nn.Conv2d 接受一个 4 维的张量,每一维分别是 sSamples x nChannels x Height x Width(样本数 x 通道数 x 高 x 宽)。如果是单个样本,需使用 input.unsqueeze(0) 来添加其它的维数解决问题。
在继续之前,我们回顾一下到目前为止用到的类。
torch.Tensor:自动调用backward()实现支持自动梯度计算的多维数组,并且保存关于这个向量的梯度。nn.Module:神经网络模块。封装参数、移动到 GPU 上运行、导出、加载等。nn.Parameter:变量,当把它赋值给一个Module时,被自动地注册为一个参数。autograd.Function:实现自动求导操作的前向和反向定义,每个变量操作至少创建一个函数节点。
至此,我们以及完成:
- 定义一个网络
- 处理输入,调用
backword。
接下来还需要:
- 计算损失。
- 更新网络权重。
损失函数
一个损失函数接受一对 (output, target) 作为输入,计算一个值来估计网络的输出和目标值相差多少。
torch.nn 中有很多不同的 损失函数。nn.MSELoss 是一个比较简单的损失函数,它可以用来计算输出和目标间的 均方误差,例如:
output = net(input)
target = torch.randn(10) # 随机值作为样例
target = target.view(1, -1) # 使 target 和 output 的 shape 相同
criterion = nn.MSELoss()
loss = criterion(output, target)
loss
当我们添加 loss 计算之后,如果使用它 .grad_fn 属性,将得到如下所示的计算图:
input → conv2d → relu → maxpool2d → conv2d → relu → maxpool2d → view → linear → relu → linear → relu → linear → MSELoss → loss
所以,当我们调用 loss.backward() 时,会针对整个图执行微分操作。图中所有具有 requires_grad=True 的张量的 .grad 梯度会被累积起来。为了说明该情况,我们回溯几个步骤:
print(loss.grad_fn) # MSELoss
print(loss.grad_fn.next_functions[0][0]) # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0]) # ReLU
反向传播
调用 loss.backward() 获得反向传播的误差。但是在调用前需要清除已存在的梯度,否则梯度将被累加到已存在的梯度。现在,我们将调用 loss.backward(),并查看 conv1 层的偏差(bias)项在反向传播前后的梯度。下方的代码只能执行一次。
net.zero_grad() # 清除梯度
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
torch.nn 中包含了各种用来构成深度神经网络构建块的模块和损失函数,你可以阅读 官方文档。
更新权重
至此,剩下的最后一件事,那就是更新网络的权重。
在实践中最简单的权重更新规则是随机梯度下降(SGD):
$$\text{weight}=\text{weight}-\text{learning rate}*\text{gradient}$$
我们可以使用简单的 Python 代码实现这个规则:
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)
当你想使用其他不同的优化方法,如 SGD、Nesterov-SGD、Adam、RMSPROP 等来更新神经网络参数时。可以借助于 PyTorch 中的 torch.optim 快速实现。使用它们非常简单:
import torch.optim as optim
# 创建优化器
optimizer = optim.SGD(net.parameters(), lr=0.01)
# 执行一次训练迭代过程
optimizer.zero_grad() # 梯度置零
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # 更新
loss
多执行几次,观察损失值的变化情况。
训练一个分类器
上面,你已经看到如何去定义一个神经网络,计算损失值和更新网络的权重。接下来,我们实现一个图像分类神经网络。
一般情况下处理图像、文本、音频和视频数据时,可以使用标准的 Python 来加载数据为 NumPy 数组。然后把这个数组转换成torch.*Tensor。
- 图像可以使用 Pillow, OpenCV。
- 音频可以使用 SciPy, librosa。
- 文本可以使用原始 Python 和 Cython 来加载,或者使用 NLTK 或 SpaCy 处理。
特别地,对于图像任务,PyTorch 提供了专门的包 torchvision,它包含了处理一些基本图像数据集的方法。这些数据集包括 Imagenet, CIFAR10, MNIST 等。除了数据加载以外,torchvision 还包含了图像转换器,torchvision.datasets 和 torch.utils.data.DataLoader 数据加载器。
torchvision 不仅提供了巨大的便利,也避免了代码的重复。接下来,我们使用 CIFAR10 数据集完成分类器训练。该数据集有如下 10 个类别:airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck。CIFAR-10 的图像都是 $3 \times 32 \times 32$ ,即 3 个颜色通道,$32 \times 32$ 像素。
训练一个图像分类器,基本流程如下:
- 使用
torchvision加载和归一化 CIFAR10 训练集和测试集。 - 定义一个卷积神经网络。
- 定义损失函数。
- 在训练集上训练网络。
- 在测试集上测试网络。
读取和归一化 CIFAR10
使用 torchvision 可以非常容易地加载 CIFAR10。torchvision 的输出是 [0,1] 的 PILImage 图像,我们把它转换为归一化范围为 [-1, 1] 的张量。
import torchvision
import torchvision.transforms as transforms
# 图像预处理步骤
transform = transforms.Compose(
[transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# 训练数据加载器
trainset = torchvision.datasets.CIFAR10(
root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(
trainset, batch_size=4, shuffle=True, num_workers=2)
# 测试数据加载器
testset = torchvision.datasets.CIFAR10(
root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(
testset, batch_size=4, shuffle=False, num_workers=2)
# 图像类别
classes = ('plane', 'car', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck')
trainloader, testloader
我们可视化其中的一些训练图像。
import matplotlib.pyplot as plt
%matplotlib inline
def imshow(img):
# 展示图像的函数
img = img / 2 + 0.5 # 反向归一化
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# 获取随机数据
dataiter = iter(trainloader)
images, labels = dataiter.next()
# 展示图像
imshow(torchvision.utils.make_grid(images))
# 显示图像标签
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
定义一个卷积神经网络
从之前的神经网络一节复制神经网络代码,并修改输入为 3 通道图像。
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
net
定义损失函数和优化器
我们使用交叉熵作为损失函数,使用带动量的随机梯度下降完成参数优化。
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
optimizer
训练网路
有趣的训练过程开始了。只需在数据迭代器上循环,将数据输入给网络,并优化。由于使用了卷积神经网络,该训练时间较长,请耐心等待。
for epoch in range(1): # 迭代一次
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# 获取输入
inputs, labels = data
# 梯度置 0
optimizer.zero_grad()
# 正向传播,反向传播,优化
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 打印状态信息
running_loss += loss.item()
if i % 200 == 199: # 每 200 批次打印一次
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 200))
running_loss = 0.0
print('Finished Training.')
在测试集上测试网络
我们在整个训练集上进行了训练,但是需要检查网络是否从数据集中学习到有用的东西。一般情况下,可以通过预测神经网络输出的类别标签与实际情况标签进行对比来进行检测。如果预测正确,我们把该样本添加到正确预测列表。
第一步,显示测试集中的图片并熟悉图片内容。
dataiter = iter(testloader)
images, labels = dataiter.next()
# 显示图片
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
让我们看看神经网络认为以上图片是什么。
outputs = net(images)
outputs
输出是 10 个标签的权重。一个类别的权重越大,神经网络越认为它是这个类别。所以让我们得到最高权重的标签。
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]] for j in range(4)))
结果看来不错。接下来让看看网络在整个测试集上的结果如何。
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d%%' %
(100 * correct / total))
结果看起来不错,至少比随机选择要好,随机选择的正确率为 10%。似乎网络学习到了一些东西。
那么,在识别哪一个类的时候好,哪一个不好呢?
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d%%' %
(classes[i], 100 * class_correct[i] / class_total[i]))
如上所示,得到了在单个类别上的预测准确度。
参考资料
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️