XGBoost 梯度提升算法入门
XGBoost 最早的雏形出现在 2014 年,当时由 陈天奇 读博期间负责的研究项目中。后经开源,逐渐发展成一个支持 C++,Java,Python,R 和 Julia 语言的成熟框架。XGBoost 是 Extreme Gradient Boosting 的缩写,其中的 Gradient Boosting 实际上就是梯度提升算法。所以在正式学习之前,我们有必要对梯度提升算法进行简单了解。
梯度提升算法
Gradient Boosting 梯度提升实际上是机器学习中的集成学习算法,实际上就是不断改进弱学习器来变成强学习器的过程,这个思想类似于三个臭皮匠顶个诸葛亮。本次试验中,我们无法从 0 开始介绍 Gradient Boosting,你需要具备一些机器学习基础。特别地,需要对机器学习中常用概念和决策树算法有所了解。如果你不具备这些基础,建议先学习蓝桥云课已有的 机器学习基础课程。
接下来,我们尽量在不涉及大量数据理论推导的前提下,解释梯度提升算法的原理和过程。
Gradient Boosting 的名字实际上由 2 部分组成:Gradient Descent + Boosting。首先需要搞清楚什么是 Boosting。Boosting 含义正如字面意思「提升」,通过对弱学习器进行改进,得到强学习器的过程,也就是提升过程。弱学习器是非常简单的模型,复杂度低,训练简单,不容易过拟合。这些模型往往也就比随意乱猜好一些,例如只有一层深度的决策树。那么,我们将选择的弱学习器称为基学习器,在此基础上进行组合得到改进之后的学习器。
通过弱学习器训练强学习器的过程实际上延续了弱学习器的一些优点,所以 Gradient Boosting 具有很好的鲁棒性,能有效避免过拟合。过拟合是机器学习中很容易掉入的陷阱。此外,Gradient Boosting 除了 Boosting 拥有的一般性质外,还能利用不同的损失函数,可以处理回归、分类等机器学习任务。
由于应用 Gradient Boosting 解决回归问题比分类问题更加简单,所以我们下面以一个回归问题为例,来简单说明一下 Gradient Boosting 的过程。
假设我们有如下所示的一组数据,我们希望利用一个弱学习器根据 $x$ 预测 $y$ 值。其中,$y$ 为真实值,$y_{-} = F(x)$ 为预测值。下面,我们选择回归树作为弱学习器,并且将树的深度限制在 1 层,以确保模型足够简单。回归树模型使用 scikit-learn 提供的函数,如果你不太熟悉 scikit-learn 的使用,可以先学习 scikit-learn 机器学习基础课程。
import numpy as np
from sklearn.tree import DecisionTreeRegressor
# 建议一个最大为 1 层的回归树弱学习器
weak_learner = DecisionTreeRegressor(max_depth=1)
x = np.array([[2], [-2], [-1], [3], [7]]) # 输入值
y = np.array([-1, 13, 5, 2, 9]) # 真实值
weak_learner.fit(x, y) # F(x) 回归树
y_ = weak_learner.predict(x) # 预测
y_
array([ 3.75, 13. , 3.75, 3.75, 3.75])接下来,我们希望利用上面的 $F(x)$ 训练出一个更好的预测模型。在这个过程中,我们不能对 $F(x)$ 进行改动。那么,我们需要利用这个弱学习器再训练一个模型 $h(x)$,加在原先的 $F(x)$ 上。此时,我们期望 $F(x) + h(x)$ 能比原本的模型 $F(x)$ 更好。
在这个过程中,我们需要一个评价指标,对于回归问题常选择 MSE 均方误差来进行评估。公式如下:
$$\mathrm{MSE}=\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-F(x_{i})\right)^{2}$$
接下来,基于公式计算 MSE 的值。
# 计算 MSE 值
np.square(np.subtract(y, y_)).mean()
10.95回归问题中,我们经常会用残差表示真实值和预测值之间的差距。所以,这里通过 $y$ 和 $y_{-} = F(x)$ 计算每个样本对应的残差。
res = y - y_
res
array([-4.75, 0. , 1.25, -1.75, 5.25])计算出每个样本的残差之后,我们可以使用弱学习器再训练一个预测残差的 $h(x)$,使 $h(x) \approx y-y_{-}$。假设弱学习器表现不错,那么就应该能得到 $F(x) + h(x) \approx y$ 了。这样就达到了上面的期望,$F(x) + h(x)$ 能比原本的模型 $F(x)$ 更好。
那么,既然想通过弱学习器训练新的 $h(x)$,使之比 $F(x)$ 更好。那么,我们的思路可以依据残差来调整真实值和预测值之间的差距,也就是使 $h(x) \approx y-y_{-}$,这样就可以使 $F(x) + h(x) \approx y$ 了。
weak_learner.fit(x, res) # h(x)
res_ = weak_learner.predict(x)
res_
array([-1.3125, -1.3125, -1.3125, -1.3125, 5.25 ])此时,我们再计算最终的残差 $y - (F(x) + h(x))$,也就是 $y - F(x) - h(x)$:
res - res_
array([-3.4375, 1.3125, 2.5625, -0.4375, 0. ])那么对于新的模型 $F(x) + h(x)$ 而言,其对应的 MSE 值为:
# 计算 MSE 值
np.square(np.subtract(res, res_)).mean()
4.059375相较于先前 $F(x)$,MSE 值减少了很多,也代表模型更好了。
至此,你大概应该能明白 Gradient Boosting 的逻辑了,也就是如果使用弱学习器来训练强学习器。总结来讲:
- 先利用弱学习器训练 $F(x)$。
- 再利用 $F(x)$ 的残差作为目标,训练 $h(x)$。
- 利用 $F(x)+h(x)$ 的残差作为目标,训练出 $m(x)$,以此类推。
- 最后 $F(x)+h(x)+m(x)+…$ 就是最终的强学习器模型。
有趣的问题出现了,既然我们在优化残差,为什么不叫 Residual Boosting,而叫 Gradient Boosting?实验一开始说 Gradient 表示 Gradient Descent 梯度下降法,哪里用了 Gradient Descent?
要解释清楚这个问题,我们回到 MSE 的公式,并简化该公式如下:
$$\mathrm{L(y, F(x))}=\frac{1}{n} \sum \left(y-F(x)\right)^{2}$$
此时,求 $F(x)$ 的偏导数:
$$\frac{\partial L}{\partial F}=- \frac{2}{n} \sum (y-F)$$
你会发现,残差 $(y-F)$,也就是 $F$ 在 $x$ 处的 Gradient 梯度乘以一个负系数。如果,我们把新的学习器 $H(x) = F(x)+h(x)$ 看作是对弱学习器 $F(x)$ 的更新过程,那么:
$$h(x) \approx y−F(x) = - \frac{n}{2} \frac{\partial L}{\partial F} = - \lambda \frac{\partial L}{\partial F}$$
$$H(x) = F(x) - \lambda \frac{\partial L}{\partial F}$$
这不正好就是 Gradient Descent 梯度下降的更新公式吗?区别于大多数机器学习方法使用 Gradient Descent 对参数更新的过程,Gradient Boosting 中的更新「参数」,实际上就是预测值 $F(x)$。
至此,我们终于搞清楚为什么梯度提升算法被称为 Gradient Boosting 了。
XGBoost 框架使用
上面,我们只是演示了一个非常简单的 Gradient Boosting 用于回归问题的例子,这只能算一个雏形。事实上,Gradient Boosting 经过不断地优化,逐渐形成了像 GBDT,GBRT 和 GBM 等算法。从 0 开始实现这些算法是非常复杂的,所以我们通常会用到 XGBoost 框架。
分类问题
XGBoost 使用起来非常方便,高效。如果你之前有使用 scikit-learn 的经验,上手该工具简直不要太简单。接下来,我们将通过几个 Toy Dataset 来学习 XGBoost 的使用技巧。首先,我们选择一个简单的分类问题:手写字符识别。同样,实验选择 scikit-learn 提供的相关函数和方法,如果你不太熟悉 scikit-learn 的使用,可以先学习 scikit-learn 机器学习基础课程。
from sklearn.datasets import load_digits
digits = load_digits() # 加载手写字符识别数据集
X = digits.data # 特征值
y = digits.target # 目标值
X.shape, y.shape
((1797, 64), (1797,))可以看到,该数据集有 1797 个样本,64 个特征。接下来,首先对数据集进行划分,划为 70% 训练数据和 30% 测试数据。
from sklearn.model_selection import train_test_split
# 划分数据集,70% 训练数据和 30% 测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
((1257, 64), (540, 64), (1257,), (540,))
然后,我们可以使用 XGBoost 建模。XGBoost 的分类器方法为 XGBClassifier。参数非常多,我们看一下常用的几个:
- max_depth – 基学习器的最大树深度。
- learning_rate – Boosting 学习率。
- n_estimators – 决策树的数量。
- gamma – 惩罚项系数,指定节点分裂所需的最小损失函数下降值。
- booster – 指定提升算法:gbtree, gblinear or dart。
- n_jobs – 指定多线程数量。
- reg_alpha – L1 正则权重。
- reg_lambda – L2 正则权重。
- scale_pos_weight – 正负权重平衡。
- random_state – 随机数种子。
接下来,我们以默认参数来初始化模型。
import xgboost as xgb
model_c = xgb.XGBClassifier()
model_c
XGBClassifier(base_score=None, booster=None, colsample_bylevel=None,
colsample_bynode=None, colsample_bytree=None, gamma=None,
gpu_id=None, importance_type='gain', interaction_constraints=None,
learning_rate=None, max_delta_step=None, max_depth=None,
min_child_weight=None, missing=nan, monotone_constraints=None,
n_estimators=100, n_jobs=None, num_parallel_tree=None,
objective='binary:logistic', random_state=None, reg_alpha=None,
reg_lambda=None, scale_pos_weight=None, subsample=None,
tree_method=None, validate_parameters=False, verbosity=None)模型的训练和测试过程和 scikit-learn 的用法非常相似。
model_c.fit(X_train, y_train) # 使用训练数据训练
model_c.score(X_test, y_test) # 使用测试数据计算准确度
0.9518518518518518可以看到,使用默认参数的分类准确度还是不错的。
回归问题
除了分类,XGBoost 当然也可以用来解决回归问题。与 XGBClassifier 相似,回归调用 XGBRegressor() 接口。由于包含的参数比较解决,我们就不再罗列了,详细内容请直接阅读官方文档。
接下来,我们那 scikit-learn 提供的 Boston 数据集进行举例。
from sklearn.datasets import load_boston
boston = load_boston()
X = boston.data # 特征值
y = boston.target # 目标值
# 划分数据集,80% 训练数据和 20% 测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
((404, 13), (102, 13), (404,), (102,))
调用 XGBRegressor() 训练模型及评估。
model_r = xgb.XGBRegressor()
model_r
XGBRegressor(base_score=None, booster=None, colsample_bylevel=None,
colsample_bynode=None, colsample_bytree=None, gamma=None,
gpu_id=None, importance_type='gain', interaction_constraints=None,
learning_rate=None, max_delta_step=None, max_depth=None,
min_child_weight=None, missing=nan, monotone_constraints=None,
n_estimators=100, n_jobs=None, num_parallel_tree=None,
objective='reg:squarederror', random_state=None, reg_alpha=None,
reg_lambda=None, scale_pos_weight=None, subsample=None,
tree_method=None, validate_parameters=False, verbosity=None)model_r.fit(X_train, y_train) # 使用训练数据训练
model_r.score(X_test, y_test) # 使用测试数据计算 R^2 评估指标
0.7859600854280273目标参数
如果你细心的话,应该可以注意到 XGBClassifier 和 XGBRegressor 中都存在一个参数 objective。解决分类问题时,默认选择了 objective='binary:logistic',而回归问题默认选择了 objective='reg:linear'。从字面意思你应该能发现,这是一个指定学习器完成哪种类型任务的参数,通常称为目标参数。
那么,该参数在解决回归问题时一般为 reg:linear(即将更名为:reg:squarederror) 和 reg:logistic,分别代表线性回归和逻辑回归。而分类则又包含 2 种情况,2 分类问题可设置为 binary:logistic(输出概率)和 binary:logitraw(类别)。多分类问题则为 multi:softmax(类别)和 multi:softprob(概率)。
细心的你可能又有疑问了,上方解决手写字符分类时是一个 10 分类问题,而默认参数为 objective='binary:logistic',该参数不是用来解决 2 分类问题吗?
实际上,当你调用 XGBClassifier,虽然你看到的是 objective='binary:logistic',但实际训练时如果是多分类问题,参数会被自动修正。我们可以通过下面的方法重新获取训练后模型的参数。
model_c.get_params()
{'objective': 'multi:softprob',
'base_score': 0.5,
'booster': None,
'colsample_bylevel': 1,
'colsample_bynode': 1,
'colsample_bytree': 1,
'gamma': 0,
'gpu_id': -1,
'importance_type': 'gain',
'interaction_constraints': None,
'learning_rate': 0.300000012,
'max_delta_step': 0,
'max_depth': 6,
'min_child_weight': 1,
'missing': nan,
'monotone_constraints': None,
'n_estimators': 100,
'n_jobs': 0,
'num_parallel_tree': 1,
'random_state': 0,
'reg_alpha': 0,
'reg_lambda': 1,
'scale_pos_weight': None,
'subsample': 1,
'tree_method': None,
'validate_parameters': False,
'verbosity': None}
你可以看到,目标参数已被修正为 'objective': 'multi:softprob'。
原生接口
上面我们介绍了 XGBoost 针对分类和回归问题的模型方法 XGBClassifier 和 XGBRegressor。实际上,如果你熟悉 scikit-learn 的话,你会发现这些接口的使用方式与 scikit-learn 的接口几乎一致。当然,XGBoost 这样设计的目的,就是让会 scikit-learn 的开发者快速上手 XGBoost。
实际上,XGBoost 还有一套原生接口,也就是按自己风格设计的函数。接下来,首先了解 XGBoost 自有的数据类型 DMatrix。
DMatrix 是一种可以同时将特征和目标值封装在一起的数据类型。该方法使用简单,不再单独罗列参数,直接演示。
# 依次传入特征和目标值
train_d = xgb.DMatrix(data=X_train, label=y_train)
test_d = xgb.DMatrix(data=X_test, label=y_test)
train_d, test_d
(<xgboost.core.DMatrix at 0x7fd8029eb390>,
<xgboost.core.DMatrix at 0x7fd8029eb358>)
XGBoost 既然想让你把特征和目标封装在一起,当然是有自己的考虑。所以,XGBoost 还提供了一个原生的训练接口 XGBoost.train。该方法的使用和上面不太一样,我们可以直接传入 DMatrix 数据,而不需要像 scikit-learn 那样分别传入特征值和目标值。
XGBoost.train 使用时,必须传入 params 和 dtrain,即学习器配置和训练数据。params 至少需要传入学习目标参数。
model_t = xgb.train(params={'objective': 'reg:squarederror'}, dtrain=train_d)
model_t
<xgboost.core.Booster at 0x7fd8029eb748>
此时,我们就可以使用像 .predict 方法进行预测,或者 .eval 方法进行模型评估。同样,需要传入 DMatrix 类型数据。
model_t.eval(test_d) # 使用测试数据进行评估
'[0]\teval-rmse:4.958941'绘制决策树
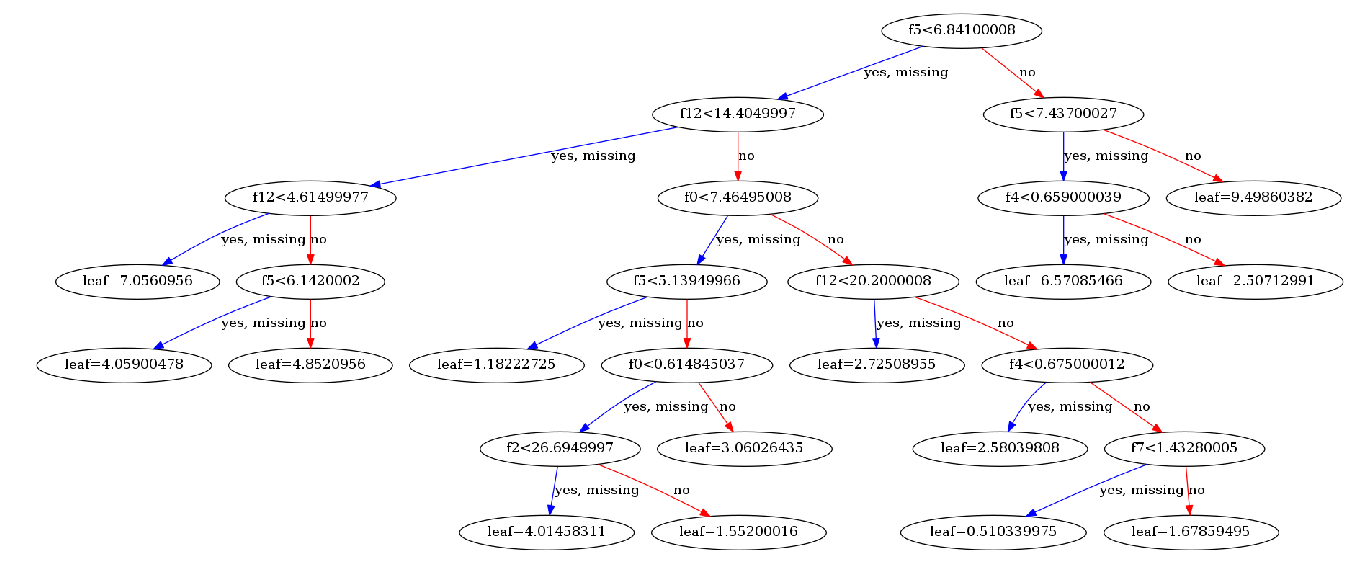
XGBoost 提供了 xgb.plot_tree 方法,可以将模型训练好之后的决策子树绘制出来。使用时,只需要传入模型和子树的序号即可,想画哪颗就画哪颗。
from matplotlib import pyplot as plt
from matplotlib.pylab import rcParams
%matplotlib inline
# 设置图像大小
rcParams['figure.figsize'] = [50, 10]
xgb.plot_tree(model_t, num_trees=1)
交叉验证
接下来,我们看一下如何使用 XGBoost 进行交叉验证。
交叉验证是机器学习中快速评估模型的重要方法。我们可以将数据集划分为 N 个子集,使用其中的 N-1 个集合训练模型,最后在剩余的 1 个子集上进行评估。依次轮询,最后求出 N 次评估的平均指标,作为该模型的最终评价结果。XGBoost 提供了 xgb.cv 方法用于完成交叉验证过程。
所以,交叉验证无需再单独划分训练和测试集,我们直接使用完整数据集即可。
# 依次传入特征和目标值
boston_d = xgb.DMatrix(data=X, label=y)
xgb.cv(dtrain=boston_d, params={'objective': 'reg:squarederror'}, nfold=5, as_pandas=True)
| train-rmse-mean | train-rmse-std | test-rmse-mean | test-rmse-std | |
|---|---|---|---|---|
| 0 | 17.105578 | 0.129116 | 17.163215 | 0.584297 |
| 1 | 12.337973 | 0.097558 | 12.519736 | 0.473458 |
| 2 | 8.994071 | 0.065756 | 9.404534 | 0.472309 |
| 3 | 6.629481 | 0.050323 | 7.250335 | 0.500342 |
| 4 | 4.954406 | 0.033209 | 5.920812 | 0.591874 |
| 5 | 3.781454 | 0.029604 | 5.045190 | 0.687971 |
| 6 | 2.947767 | 0.038786 | 4.472030 | 0.686492 |
| 7 | 2.357748 | 0.042040 | 4.179314 | 0.737935 |
| 8 | 1.951907 | 0.044972 | 3.979878 | 0.798198 |
| 9 | 1.660895 | 0.044894 | 3.870751 | 0.812331 |
上方参数中,dtrain 传入数据集,params 为模型自定义参数,nfold 为交叉验证划分的 N 个子集,as_pandas 则表示最终以 DataFrame 样式输出。默认情况下,XGBoost 会执行 Boosting 迭代 10 次,所以你可以看到 10 行输出。当然,你可以修改 num_boost_round 参数,自定义最大迭代次数。
至此,我们已经完成了梯度提升算法和 XGBoost 的使用学习。希望大家在使用过程中,多结合 官方文档,了解更为细节和更新的内容。
相关链接
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️