TensorFlow 2.0 实现线性回归
线性回归是机器学习中最简单的问题,同时线性回归也与人工神经网络有千丝万缕的关系。文章中,我们将以线性回归为例,使用 TensorFlow 2.0 提供的 API 来进行实现。与此同时,我们会使用 1.x API 与之对比。
线性回归是入门机器学习必学的算法,其也是最基础的算法之一。接下来,我们以线性回归为例,使用 TensorFlow 2.0 提供的 API 和 Eager Execution 机制对其进行实现。
低阶 API 实现
低阶 API 实现,实际上就是利用 Eager Execution 机制来完成。实验首先初始化一组随机数据样本,并添加噪声,然后将其可视化出来。
import matplotlib.pyplot as plt
import tensorflow as tf
%matplotlib inline
TRUE_W = 3.0
TRUE_b = 2.0
NUM_SAMPLES = 100
# 初始化随机数据
X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
y = X * TRUE_W + TRUE_b + noise # 添加噪声
plt.scatter(X, y)
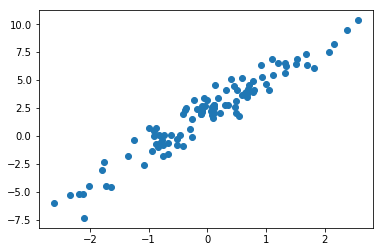
接下来,我们定义一元线性回归模型。
$$f(w, b, x) = w*x + b$$
这里我们构建自定义模型类,并使用 TensorFlow 提供的 tf.Variable 随机初始化参数 $w$ 和截距项 $b$。
class Model(object):
def __init__(self):
self.W = tf.Variable(tf.random.uniform([1])) # 随机初始化参数
self.b = tf.Variable(tf.random.uniform([1]))
def __call__(self, x):
return self.W * x + self.b # w*x + b
对于随机初始化的 $w$ 和 $b$,我们可以将其拟合直线绘制到样本散点图中。
model = Model() # 实例化模型
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
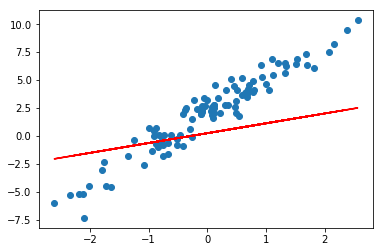
可以明显看出,直线并没有很好地拟合样本。当然,由于是随机初始化,也有极小概率一开始拟合效果非常好,那么重新执行一次上面的单元格另外随机初始化一组数据即可。
然后,我们定义线性回归使用到的损失函数。这里使用线性回归问题中常用的平方损失函数。对于线性回归问题中与数学相关的知识点,本次实验不再推动和讲解。
$${\rm Loss}(w, b, x, y) = \sum_{i=1}^N (f(w, b, x_i) - y_i)^2$$
根据公式实现损失计算函数。
def loss_fn(model, x, y):
y_ = model(x)
return tf.reduce_mean(tf.square(y_ - y))
接下来,就可以开始迭代过程了,这也是最关键的一步。使用迭代方法求解线性回归的问题中,我们首先需要计算参数的梯度,然后使用梯度下降法来更新参数。
公式中,$lr$ 指代学习率。
TensorFlow 2.0 中的 Eager Execution 提供了 tf.GradientTape 用于追踪梯度。所以,下面我们就实现梯度下降法的迭代更新过程。
EPOCHS = 10
LEARNING_RATE = 0.1
for epoch in range(EPOCHS): # 迭代次数
with tf.GradientTape() as tape: # 追踪梯度
loss = loss_fn(model, X, y) # 计算损失
dW, db = tape.gradient(loss, [model.W, model.b]) # 计算梯度
model.W.assign_sub(LEARNING_RATE * dW) # 更新梯度
model.b.assign_sub(LEARNING_RATE * db)
# 输出计算过程
print('Epoch [{}/{}], loss [{:.3f}], W/b [{:.3f}/{:.3f}]'.format(epoch, EPOCHS, loss,
float(model.W.numpy()),
float(model.b.numpy())))
Epoch [0/10], loss [9.949], W/b [1.395/0.608]
Epoch [1/10], loss [6.420], W/b [1.791/0.899]
Epoch [2/10], loss [4.270], W/b [2.097/1.132]
Epoch [3/10], loss [2.957], W/b [2.332/1.318]
Epoch [4/10], loss [2.156], W/b [2.514/1.466]
Epoch [5/10], loss [1.665], W/b [2.653/1.585]
Epoch [6/10], loss [1.365], W/b [2.761/1.680]
Epoch [7/10], loss [1.180], W/b [2.845/1.756]
Epoch [8/10], loss [1.067], W/b [2.909/1.817]
Epoch [9/10], loss [0.998], W/b [2.958/1.865]
上面的代码中,我们初始化 tf.GradientTape() 以追踪梯度,然后使用 tape.gradient 方法就可以计算梯度了。值得注意的是,tape.gradient() 第二个参数支持以列表形式传入多个参数同时计算梯度。紧接着,使用 .assign_sub 即可完成公式中的减法操作用以更新梯度。
最终,我们绘制参数学习完成之后,模型的拟合结果。
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
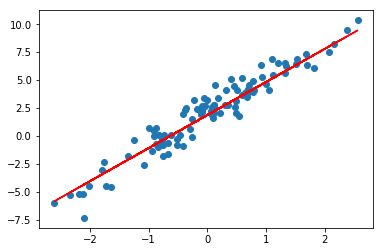
如无意外,你将得到一个比随机参数好很多的拟合直线。
提示:由于是随机初始化参数,如果迭代后拟合效果仍然不好,一般是迭代次数太少的原因。你可以重复执行上面的迭代单元格多次,增加参数更新迭代次数,即可改善拟合效果。此提示对后面的内容同样有效。
高阶 API 实现
TensorFlow 2.0 中提供了大量的高阶 API 帮助我们快速构建所需模型,接下来,我们使用一些新的 API 来完成线性回归模型的构建。这里还是沿用上面提供的示例数据。
tf.keras 模块下提供的 tf.keras.layers.Dense 全连接层(线性层)实际上就是一个线性计算过程。所以,模型的定义部分我们就可以直接实例化一个全连接层即可。
model = tf.keras.layers.Dense(units=1) # 实例化线性层
其中,units 为输出空间维度。此时,参数已经被初始化了,所以我们可以绘制出拟合直线。
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
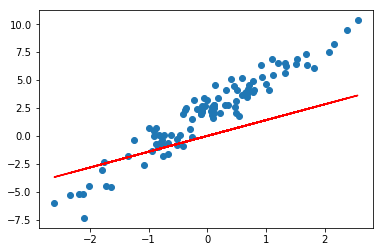
你可以使用 model.variables 打印出模型初始化的随机参数。
model.variables
[<tf.Variable 'dense/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[1.4135073]], dtype=float32)>,
<tf.Variable 'dense/bias:0' shape=(1,) dtype=float32, numpy=array([0.], dtype=float32)>]接下来就可以直接构建模型迭代过程了。
这里同样使用 tf.GradientTape() 来追踪梯度,我们简化损失计算和更新的过程。首先,损失可以使用现有 API tf.keras.losses.mean_squared_error 计算,最终使用 tf.reduce_sum 求得全部样本的平均损失。
EPOCHS = 10
LEARNING_RATE = 0.002
for epoch in range(EPOCHS): # 迭代次数
with tf.GradientTape() as tape: # 追踪梯度
y_ = model(X)
loss = tf.reduce_sum(tf.keras.losses.mean_squared_error(y, y_)) # 计算损失
grads = tape.gradient(loss, model.variables) # 计算梯度
optimizer = tf.keras.optimizers.SGD(LEARNING_RATE) # 随机梯度下降
optimizer.apply_gradients(zip(grads, model.variables)) # 更新梯度
print('Epoch [{}/{}], loss [{:.3f}]'.format(epoch, EPOCHS, loss))
Epoch [0/10], loss [848.794]
Epoch [1/10], loss [339.506]
Epoch [2/10], loss [172.200]
Epoch [3/10], loss [116.692]
Epoch [4/10], loss [98.099]
Epoch [5/10], loss [91.816]
Epoch [6/10], loss [89.674]
Epoch [7/10], loss [88.938]
Epoch [8/10], loss [88.684]
Epoch [9/10], loss [88.596]
其次,使用 model.variables 即可读取可参数的列表,无需像上面那样手动传入。这里不再按公式手动更新梯度,而是使用现有的随机梯度下降函数 tf.keras.optimizers.SGD,然后使用 apply_gradients 即可更新梯度。
最终,同样将迭代完成的参数绘制拟合直线到原图中。
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
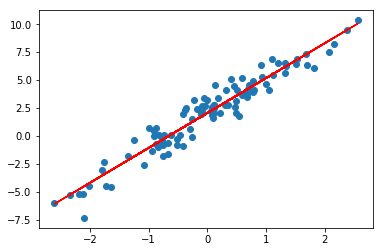
如果拟合效果不好,请参考上文提示。
Keras 方式实现
上面的高阶 API 实现过程实际上还不够精简,我们可以完全使用 TensorFlow Keras API 来实现线性回归。
我们这里使用 Keras 提供的 Sequential 序贯模型结构。和上面的例子相似,向其中添加一个线性层。不同的地方在于,Keras 序贯模型第一层为线性层时,规定需指定输入维度,这里为 input_dim=1。
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
model.summary() # 查看模型结构
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1) 2
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________
接下来,直接使用 .compile 编译模型,指定损失函数为 MSE 平方损失,优化器选择 SGD 随机梯度下降。然后,就可以使用 .fit 传入数据开始迭代了。
model.compile(optimizer='sgd', loss='mse')
model.fit(X, y, steps_per_epoch=1000)
1000/1000 [==============================] - 1s 1ms/step - loss: 5.9901
steps_per_epoch 只的是在默认小批量为 32 的条件下,传入相应次数的小批量样本。最终绘制出迭代完成的拟合图像。
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
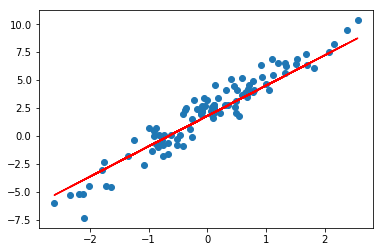
如果拟合效果不好,请参考上文提示。
如上所示,完全使用 Keras 高阶 API 实际上只需要 4 行核心代码即可完成。相比于最开始的低阶 API 简化了很多。
TensorFlow 1.x 实现
为了与 TensorFlow 2.0 线性回归实现过程进行对比。最终,我们给出 TensorFlow 1.x 线性回归实现代码。这里,我们需要实验 TensorFlow 2.0 中 tensorflow.compat.v1 模块下提供的兼容性代码。
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior() # 关闭 Eager Execution 特性
接下来,就可以使用 TensorFlow 1.x 中提供的图与会话方式来实现线性回归过程了。
X_train = tf.placeholder(tf.float32) # 定义占位符张量
y_train = tf.placeholder(tf.float32)
W = tf.Variable(tf.random.normal([1])) # 初始化参数
b = tf.Variable(tf.random.normal([1]))
LEARNING_RATE = 0.001 # 学习率
y_train_ = W*X_train + b # 线性函数
loss = tf.reduce_mean(tf.square(y_train_ - y_train)) # 平方损失函数
optimizer = tf.train.GradientDescentOptimizer(
LEARNING_RATE).minimize(loss) # 梯度下降优化损失函数
EPOCHS = 1000 # 迭代次数
with tf.Session() as sess: # 启动会话
tf.global_variables_initializer().run() # 初始化全局变量
for epoch in range(EPOCHS): # 迭代优化
sess.run(optimizer, feed_dict={X_train:X, y_train:y})
final_weight = sess.run(W) # 最终参数
final_bias = sess.run(b)
print(final_weight, final_bias)
[2.7856345] [1.6973654]最后,我们依据迭代更新的参数,将拟合直线绘制到原图中。
preds = final_weight * X + final_bias # 计算预测值
plt.scatter(X, y)
plt.plot(X, preds, c='r')
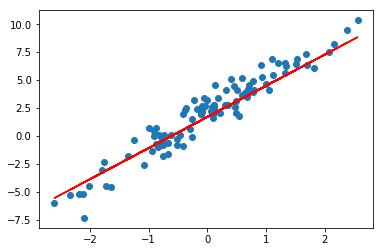
关联阅读
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️

