谱聚类及其他聚类方法应用
介绍
前面的文章中,我们已经学习了最典型的 3 类聚类方法。本周的最后一课将会带大家继续学习几种比较常见的聚类方法以帮助大家更加充分地了解聚类。
知识点
- 谱聚类
- 拉普拉斯矩阵
- 无向图切图
- 亲和传播聚类
- Mean Shift
谱聚类
谱聚类(Spectral Clustering)是一种比较年轻的聚类方法,它于 2006 年由 Ulrike von Luxburg 公布在论文 A Tutorial on Spectral Clustering 上。
如果你第一次听说这种聚类方法,应该还处于一头雾水的状态。不必担心,谱聚类是一种非常「靠谱」的聚类算法,它兼具了高效与简洁。当然,简洁的方法不一定意味着它很简单。由于谱聚类涉及到图论及矩阵分析等相关数学知识,理解起来还是不太容易的。不过,也无需过度担心,接下来将带你深入学习这种方法。
无向图
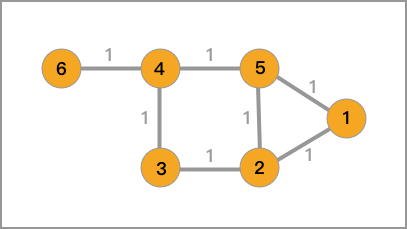
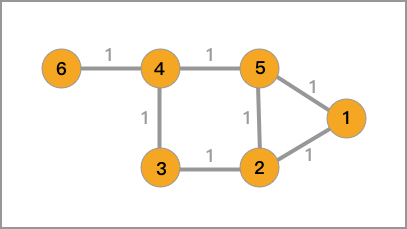
无向图,图论中最基础的概念之一,一个听起来很高级的名词,但是你已经在密度聚类文章中讲解 HDBSCAN 方法的内容中见过了。具体来讲,就是我们把平面/空间中的数据点通过直线连接起来。
那么,对应一个无向图,一般通过 $G\left ( V,E \right )$ 表示,其中,包含点的集合 $V$ 和边的集合 $E$。
拉普拉斯矩阵
接下来,我们要介绍另一个重要的概念:拉普拉斯矩阵,这也是谱聚类的核心概念。
拉普拉斯矩阵(Laplacian Matrix),也称为基尔霍夫矩阵,是无向图的一种矩阵表示形式。对于一个有 $n$ 个顶点的图,其拉普拉斯矩阵定义为:
其中,$D$ 为图的度矩阵,$A$ 为图的邻接矩阵。
度矩阵
对于有边连接的两个点 $v_i$ 和 $v_j$,$w_{ij}>0$,对于没有边连接的两个点 $v_i$ 和 $v_j$,$w_{ij}=0$。对于图中的任意一个点 $v_i$,它的度$d_i$定义为和它相连的所有边的权重之和,即
度矩阵是一个对角矩阵,主角线上的值由对应的顶点的度组成。
邻接矩阵
对于一张有 $n$ 个顶点的图 $L_{n \times n}$,其邻接矩阵 $A$ 为任意两点之间的权重值 $w_{ij}$ 组成的矩阵:
对于构建邻接矩阵 $A$,一般有三种方法,分别是:$\epsilon $-邻近法,全连接法和 K-近邻法。
第一种方法,$\epsilon $-邻近法通过设置了一个阈值 $\epsilon $,再求解任意两点 $x_{i}$ 和 $x_{j}$ 间的欧式距离 $s_{ij}$ 来度量相似性。然后,根据 $s_{ij}$ 和 $\epsilon $ 的大小关系,定义 $w_{ij}$ 如下:
第二种方法,全连接法通过选择不同的核函数来定义边权重,常用的有多项式核函数,高斯核函数和 Sigmoid 核函数。例如,当使用高斯核函数 RBF 时,$w_{ij}$ 定义如下:
除此之外,K-邻近法也可以被用于生成邻接矩阵。当我们令 $x_i$ 对应图中的一个节点 $v_i$ 时,如果 $v_j$ 属于 $v_i$ 的前 $k$ 个最近邻节点集合,则连接 $v_j$ 和 $v_i$。
但是,此种方法会产生不对称的有向图。因此,将有向图转换为无向图的方法有两种:
第一,忽略方向性,即如果 $v_j$ 属于 $v_i$ 的前 $k$ 个最近邻节点集,或$v_i$ 属于 $v_j$ 的前 $k$ 个最近邻节点集,则连接 $v_j$ 和 $v_i$。
第二是当且仅当 $v_j$ 属于 $v_i$ 的前 $k$ 个最近邻节点集,且 $v_i$ 属于 $v_j$ 的前 $k$ 个最近邻节点集时连接 $v_j$ 和 $v_i$。第二种方法体现了相互性。
那么,对于 1.1 中的无向图,它对应的邻接矩阵、度矩阵以及拉普拉斯矩阵如下。
邻接矩阵为:
度矩阵为:
拉普拉斯矩阵为:
无向图切图
目前,通过上面了解到的方法,我们就可以生成数据集的无向图,以及其对应的拉普拉斯矩阵。
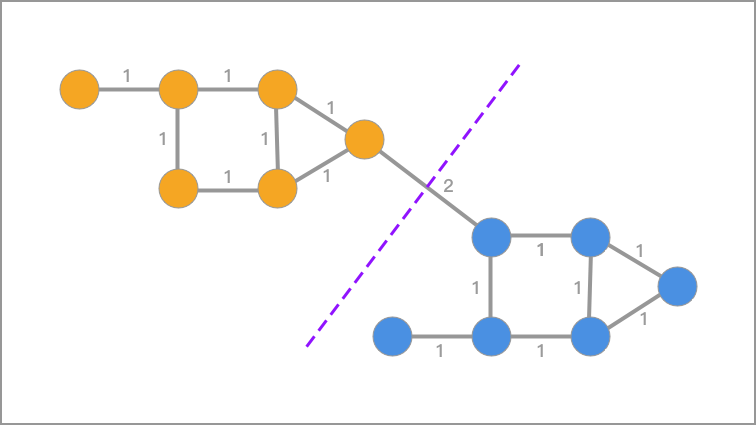
你应该可以想到,聚类其实就是寻求一种把整个无向图切分成小块的过程,而切分出来的小块就是每一个类别(簇)。所以,谱聚类的目标是将无向图划分为两个或多个子图,使得子图内部节点相似而子图间节点相异,从而达到聚类的目的。
对于无向图 G 的切图,我们的目标是将图 $G(V,E)$ 切成相互没有连接的 $k$ 个子图,每个子图点的集合为:$A_1, A_2, \cdots, A_k$,它们满足$A_i \cap A_j = \varnothing $,且 $A_1 \cup A_2 \cup \cdots \cup A_k = V$.
对于任意两个子图点的集合 $A, B \subset V$, $A \cap B=\varnothing$, 我们定义 $A$ 和 $B$ 之间的切图权重为:
那么,对于 $k$ 个子图点的集合:$A_1, A_2, \cdots, A_k$ 定义切图为:
其中 $\overline{A}_i$ 为 $A_i$ 的补集,意为除 $A_i$ 子集外其他 $V$ 的子集的并集。
容易看出,$cut(A_1,A_2,\cdots, A_k)$ 描述了子图之间的相似性,其值越小则代表子图的差异性越大。但是,公式(11)在划分子图时并没有考虑到子图最少节点的数量,这就容易导致一个数据点或者很少的数据点被划为一个独立的子图,但这明显是不正确的。
为了接近这个问题,我们会引入一些正则化方法,其中最常用的就是 RatioCut 和 Ncut。
RatioCut 切图时不光考虑最小化 $cut(A_1,A_2,\cdots, A_k)$ ,它还同时考虑最大化每个子图点的个数,其定义如下:
其中,$|A_i|$ 表示子图 $A_i$ 中节点的个数。
Ncut 切图和 RatioCut 切图很类似,但是把 Ratiocut 的分母 $|A_i|$ 换成 ${assoc(A_i)}$. 由于子图样本的个数多并不一定权重就大,我们切图时基于权重也更合我们的目标,因此一般来说 Ncut 切图优于 RatioCut 切图。
其中,${assoc(A_i, V)} = \sum_{V_j\in A_i}^{k} d_j$,$d_j = \sum_{i=1}^{n} w_{ji}$。
关于 Ncut 切图和 RatioCut 切图的推导过程因为比较复杂,暂时不予讲解。
谱聚类流程及实现
前面做了这么多知识铺垫,最后再来说一下谱聚类的流程:
- 根据数据构造无向图 $G$,图中的每一个节点对应一个数据点,将相似的点连接起来,并且边的权重用于表示数据之间的相似度。
- 计算图的邻接矩阵 $A$ 和度矩阵 $D$,并求解对应的拉普拉斯矩阵 $L$。
- 求出 $L$ 的前 $k$ 个由小到大排列的特征值${\lambda}_{i=1}^k$以及对应的特征向量${v}_{i=1}^k$。
- 把 $k$ 个特征向量排列在一起组成一个 $N\times k$ 的矩阵,将其中每一行看作 $k$ 维空间中的一个向量,并使用 K-Means 算法进行聚类,并得到最终的聚类类别。
看到上面的 4 个步骤,你会发现谱聚类的最后还是会用到 K-Means,那谱矩阵的本质是什么呢?
在我看来,谱聚类的本质就是通过拉普拉斯矩阵变换得到其特征向量组成的新矩阵的 K-Means 聚类,而其中的拉普拉斯矩阵变换可以被简单地看作是降维的过程。
而谱聚类中的「谱」其实就是矩阵中全部特征向量的总称。
下面,我们就按照谱聚类流程,并使用 Python 对谱聚类进行实现,首先生成一组示例数据。这一次,我们使用 make_circles() 生成环状数据。
from sklearn import datasets
from matplotlib import pyplot as plt
%matplotlib inline
noisy_circles, _ = datasets.make_circles(
n_samples=300, noise=0.1, factor=.3, random_state=10)
plt.scatter(noisy_circles[:, 0], noisy_circles[:, 1], color='b')
对于这组数据,我们使用 K-Means 聚成 2 类试一试。
from sklearn.cluster import KMeans
plt.scatter(noisy_circles[:, 0], noisy_circles[:, 1],
c=KMeans(n_clusters=2).fit_predict(noisy_circles))
可以看到,结果非常的不理想。于是,我们尝试通过谱聚类来完成。
参考上面的谱聚类流程,我们知道首先需要计算由数据生成无向图的邻接矩阵 $A$,这篇文章使用 K-近邻方法计算无向图中边对应的相似度权重。下面通过 knn_similarity_matrix(data, k) 函数实现:
import numpy as np
def knn_similarity_matrix(data, k):
zero_matrix = np.zeros((len(data), len(data)))
w = np.zeros((len(data), len(data)))
for i in range(len(data)):
for j in range(i + 1, len(data)):
zero_matrix[i][j] = zero_matrix[j][i] = np.linalg.norm(
data[i] - data[j]) # 计算欧式距离
for i, vector in enumerate(zero_matrix):
vector_i = np.argsort(vector)
w[i][vector_i[1: k + 1]] = 1
# 将两点间权重相加求平均
w = (np.transpose(w) + w)/2
return w
得到邻接矩阵 $A$,就可以计算得到度矩阵 $D$,以及对应的拉普拉斯矩阵 $L$,进而实现整个谱聚类方法:
def spectral_clustering(data, k, n):
# 计算近邻矩阵、度矩阵、拉普拉斯矩阵
A_matrix = knn_similarity_matrix(data, k)
D_matrix = np.diag(np.power(np.sum(A_matrix, axis=1), -0.5))
L_matrix = np.eye(len(data)) - np.dot(np.dot(D_matrix, A_matrix), D_matrix)
# 计算特征值和特征向量
eigvals, eigvecs = np.linalg.eig(L_matrix)
# 选择前 n 个最小的特征向量
indices = np.argsort(eigvals)[: n]
k_eigenvectors = eigvecs[:, indices]
k_eigenvectors
# 使用 K-Means 完成聚类
clusters = KMeans(n_clusters=n).fit_predict(k_eigenvectors)
return clusters
上面的算法实现过程中,我们并没有使用 $L = D - A$ 来计算拉普拉斯矩阵,而是使用了 归一化的拉普拉斯算子:
最后,我们定义参数 k=5, 并将数据集聚为 2 类。
sc_clusters = spectral_clustering(noisy_circles, k=5, n=2)
sc_clusters
根据聚类标签可视化数据集,可以看到谱聚类的效果是非常不错的。
plt.scatter(noisy_circles[:, 0], noisy_circles[:, 1], c=sc_clusters)
scikit-learn 中的谱聚类
scikit-learn 同样提供了谱聚类的实现方法,具体为 sklearn.cluster.SpectralClustering():
sklearn.cluster.SpectralClustering(n_clusters=8, eigen_solver=None, random_state=None, n_init=10, gamma=1.0, affinity='rbf', n_neighbors=10, eigen_tol=0.0, assign_labels='kmeans', degree=3, coef0=1, kernel_params=None, n_jobs=1)
其主要参数有:
- n_clusters:聚类簇数量。 - eigen_solver:特征值求解器。 - gamma:affinity 使用核函数时的核函数系数。 - affinity:邻接矩阵计算方法,可选择核函数、k-近邻等。 - n_neighbors:邻接矩阵选择 k-近邻法时的 k 值。 - assign_labels:最终聚类方法,默认为 K-Means。
谱聚类在很多时候会被用于图像分割,所以下面我们尝试使用谱聚类的 scikit-learn 实现来完成一个有趣的例子。该例子参考自 scikit-learn 官方文档。
首先,我们需要生成一幅示例图像,图像中有几个大小不等的圆,且存在噪点。
# 生成 100px * 100px 的图像
l = 100
x, y = np.indices((l, l))
# 在图像中添加 4 个圆
center1 = (28, 24)
center2 = (40, 50)
center3 = (67, 58)
center4 = (24, 70)
radius1, radius2, radius3, radius4 = 16, 14, 15, 14
circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2
circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2
circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2
circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2
img = circle1 + circle2 + circle3 + circle4
mask = img.astype(bool)
img = img.astype(float)
# 添加随机噪声点
img += 1 + 0.2 * np.random.randn(*img.shape)
plt.figure(figsize=(5, 5))
plt.imshow(img)
接下来,我们使用谱聚类方法完成图像边缘检测,并得到处理后的图像。
from sklearn.feature_extraction import image
from sklearn.cluster import spectral_clustering
graph = image.img_to_graph(img, mask=mask) # 图像处理为梯度矩阵
graph.data = np.exp(-graph.data / graph.data.std()) # 正则化
labels = spectral_clustering(graph, n_clusters=4)
label_im = -np.ones(mask.shape)
label_im[mask] = labels
plt.figure(figsize=(5, 5))
plt.imshow(label_im)
谱聚类的优势
谱聚类演化于图论,是一种原理简洁且效果不错的聚类方法。相比于 K-Means,谱聚类主要有以下优点。
- 适用于各类形状的数据分布聚类。
- 计算速度较快,尤其是在大数据集上明显优于其他算法。
- 避免了 K-Means 会将少数离群点划为一类的现象。
D. Cai 等 DOI: 10.1109/TKDE.2005.198 曾经在 TDT2 和 Reuters-21578 基准聚类数据集上测试过谱聚类和 K-Means 的聚类准确率表现,结果如下:
| TDT2 | Reuters-21578 | |||
|---|---|---|---|---|
| k 值 | K-Means | 谱聚类 | K-Means | 谱聚类 |
| 2 | 0.989 | 0.998 | 0.871 | 0.923 |
| 3 | 0.974 | 0.996 | 0.775 | 0.816 |
| 4 | 0.959 | 0.996 | 0.732 | 0.793 |
| … | … | … | … | … |
| 9 | 0.852 | 0.984 | 0.553 | 0.625 |
| 10 | 0.835 | 0.979 | 0.545 | 0.615 |
可以看出,谱聚类的表现普遍优于 K-Means。
当然,谱聚类也有一些缺点。例如,由于最后使用的 K-Means 聚类,所以要提前指定聚类数量。另外,当使用 K-近邻生成邻接矩阵时还需要指定最近邻样本数量,对参数是比较敏感的。
最后,我们再简单介绍几种前面没有提到的聚类方法。
亲和传播聚类
亲和传播聚类的英文名为 Affinity Propagation。Affinity Propagation 是基于数据点进行消息传递的理念设计的。与 K-Means 等聚类算法不同的地方在于,亲和传播聚类同样不需要提前确定聚类的数量,即 K 值。但由于 Affinity Propagation 运行效率较低,不太适合于大数据集聚类。
scikit-learn 中提供了 Affinity Propagation 的实现类:
sklearn.cluster.AffinityPropagation(damping=0.5, max_iter=200, convergence_iter=15, copy=True, preference=None, affinity='euclidean', verbose=False)
其主要参数有:
- damping:阻尼因子,避免数值振荡。 - max_iter:最大迭代次数。 - affinity:亲和评价方法,默认为欧式距离。
- 你可以通过 此页面 查看 Affinity Propagation 的论文、用例及源代码。
Mean Shift
Mean Shift 又被称为均值漂移聚类。Mean Shift 聚类的目的是找出最密集的区域,同样也是一个迭代过程。在聚类过程中,首先算出初始中心点的偏移均值,将该点移动到此偏移均值,然后以此为新的起始点,继续移动,直到满足最终的条件。Mean Shift 也引入了核函数,用于改善聚类效果。除此之外,Mean Shift 在图像分割,视频跟踪等领域也有较好的应用。
scikit-learn 中提供了 MeanShift 的实现类:
MeanShift(bandwidth=None, seeds=None, bin_seeding=False, min_bin_freq=1, cluster_all=True, n_jobs=1)
聚类方法选择
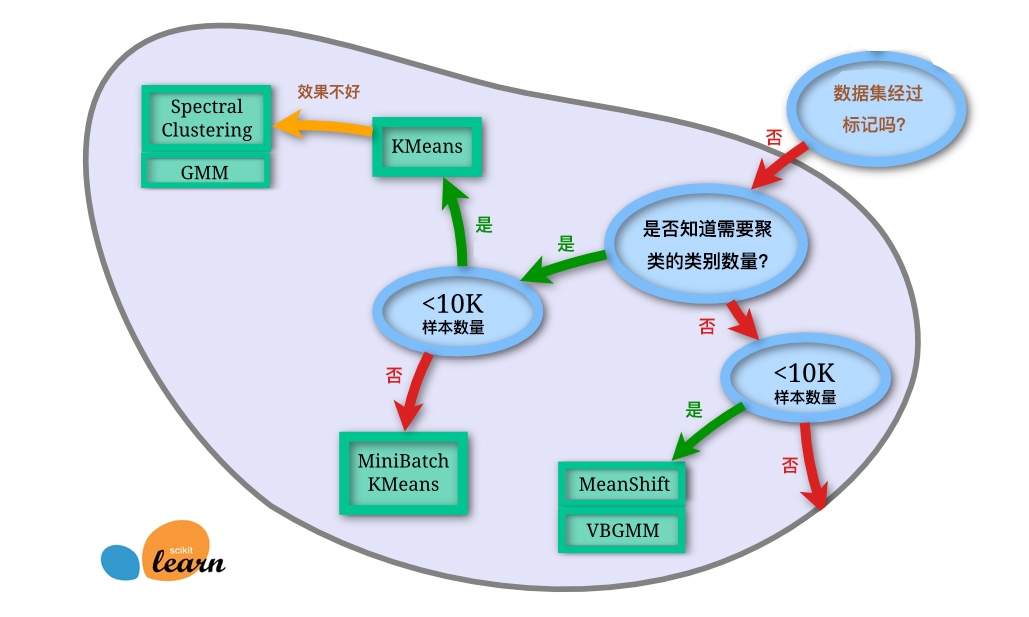
本周的内容中,我们介绍了近十种不同的聚类算法。其中,有经典的 K-Means,高效的 MiniBatchKMeans,无需指定类别的层次和密度聚类,以及适用于图像分割的谱聚类。对于这些算法,在实际应用中该如何选择呢?下面给出 scikit-learn 提供的一张图参考:
当然,上图也仅供参考,面对实际应用中的复杂情形,还需要根据具体情况而定。
小结
这篇文章主要介绍了谱聚类算法,谱聚类其实在实际运用中还是非常常见的,但很大的硬伤是不适合于大规模数据,因为计算矩阵的特征值和特征向量会非常耗时。最后介绍的亲和传播和 Mean Shift 聚类就一带而过了,因为这两种算法其实相比于我们前面介绍过的聚类算法没有明显的优势。
相关链接
系列文章
- 综述及示例
- 线性回归实现与应用
- 多项式回归实现与应用
- 岭回归和 LASSO 回归实现
- 回归模型评价与检验
- 逻辑回归实现与应用
- K-近邻算法实现与应用
- 朴素贝叶斯实现及应用
- 分类模型评价方法
- 支持向量机实现与应用
- 决策树实现与应用
- 装袋和提升集成学习方法
- 划分聚类方法实现与应用
- 层次聚类方法实现与应用
- 主成分分析原理及应用
- 密度聚类方法实现与应用
- 谱聚类及其他聚类方法应用
- 自动化机器学习综述
- 自动化机器学习实践应用
- 模型动态增量训练
- 模型推理与部署
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️