决策树实现与应用
介绍
决策树是机器学习中简单又经典的算法,这篇文章将带领大家学习决策树的原理,通过代码详细了解决策分类的特征选择,通过 Python 实现决策树的算法流程,并学习使用 scikit-learn 构建决策树模型,最后使用该模型对真实数据进行分类预测。
知识点
- 决策树算法原理
- 信息增益
- 决策树算法实现
- 学生成绩分类预测
- 决策树可视化
什么是决策树
决策树是一种特殊的树形结构,一般由节点和有向边组成。其中,节点表示特征、属性或者一个类,而有向边包含判断条件。决策树从根节点开始延伸,经过不同的判断条件后,到达不同的子节点。而上层子节点又可以作为父节点被进一步划分为下层子节点。一般情况下,我们从根节点输入数据,经过多次判断后,这些数据就会被分为不同的类别。这就构成了一颗简单的分类决策树。
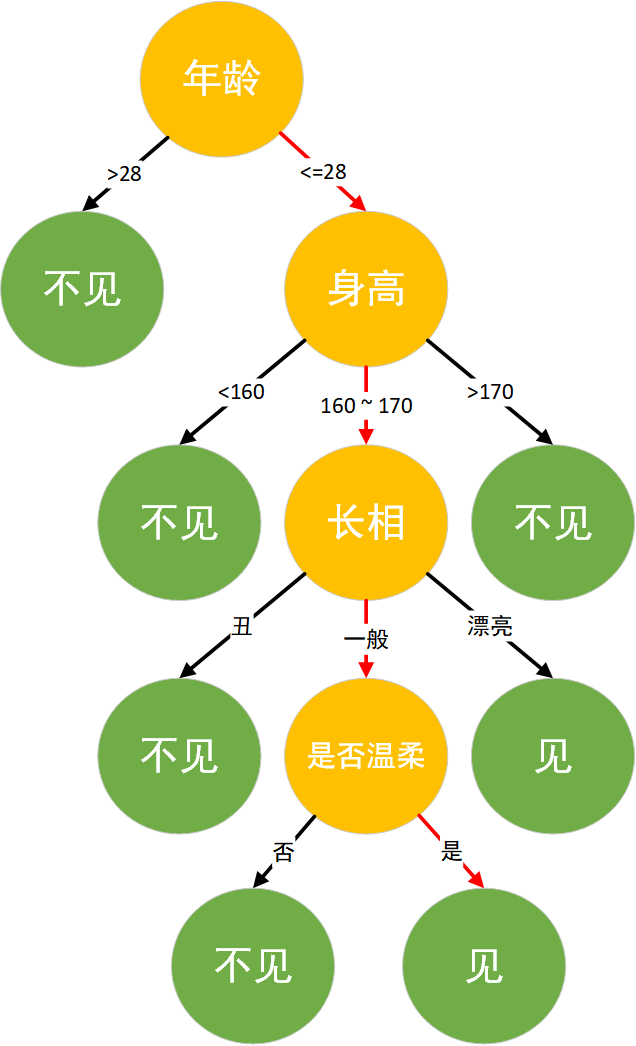
举一个通俗的例子,假设工作多年仍然单身的小楼和他母亲在给他介绍对象时的一段对话:
母亲:小楼,你都 28 了还是单身,明天亲戚家要来个姑娘要不要去见见。
小楼:多大年纪?
母亲:26。
小楼:有多高?
母亲:165 厘米。
小楼:长的好看不。
母亲:还行,比较朴素。
小楼:温柔不?
母亲:看起来挺温柔的,很有礼貌。
小楼:好,去见见。
作为程序员的小楼的思考逻辑就是典型的决策树分类逻辑,将年龄,身高,长相,是否温柔作为特征,并最后对见或者不见进行决策。其决策逻辑如图所示:
决策树算法原理
其实决策树算法如同上面场景一样,其思想非常容易理解,具体的算法流程为:
- 数据准备 → 通过数据清洗和数据处理,将数据整理为没有缺省值的向量。
- 寻找最佳特征 → 遍历每个特征的每一种划分方式,找到最好的划分特征。
- 生成分支 → 划分成两个或多个节点。
- 生成决策树 → 对分裂后的节点分别继续执行 2-3 步,直到每个节点只有一种类别。
- 决策分类 → 根据训练决策树模型,将预测数据进行分类。
下面我们依照决策树的算法流程,用 Python 来实现决策树构建和分类。首先生成一组数据,数据包含两个类别 man 和 woman,特征分别为:hair(头发长短),voice(声音粗细),height(身高),ear_stud(是否带有耳钉)。
import numpy as np
import pandas as pd
def create_data():
# 生成示例数据
data_value = np.array(
[['long', 'thick', 175, 'no', 'man'],
['short', 'medium', 168, 'no', 'man'],
['short', 'thin', 178, 'yes', 'man'],
['short', 'thick', 172, 'no', 'man'],
['long', 'medium', 163, 'no', 'man'],
['short', 'thick', 180, 'no', 'man'],
['long', 'thick', 173, 'yes', 'man'],
['short', 'thin', 174, 'no', 'man'],
['long', 'thin', 164, 'yes', 'woman'],
['long', 'medium', 158, 'yes', 'woman'],
['long', 'thick', 161, 'yes', 'woman'],
['short', 'thin', 166, 'yes', 'woman'],
['long', 'thin', 158, 'no', 'woman'],
['short', 'medium', 163, 'no', 'woman'],
['long', 'thick', 161, 'yes', 'woman'],
['long', 'thin', 164, 'no', 'woman'],
['short', 'medium', 172, 'yes', 'woman']])
columns = np.array(['hair', 'voice', 'height', 'ear_stud', 'labels'])
data = pd.DataFrame(data_value.reshape(17, 5), columns=columns)
return data
在创建好数据之后,加载并打印出这些数据
data = create_data()
data
在得到数据后,根据算法流程,接下来需要寻找最优的划分特征,随着划分的不断进行,我们尽可能的将划分的分支所包含的样本归于同一类别,即结点的「纯度」越来越高。而常用的特征划分方式为信息增益和增益率。
信息增益(ID3)
在介绍信息增益之前,先引入「信息熵」的概念。信息熵是度量样本纯度最常用的一种指标,其公式为:
其中 $\operatorname{D}$ 表示样本集合,$p_{k}$ 表示第 $k$ 类样本所占的比例。其中 $\operatorname{Ent}(\operatorname{D})$ 的值越小,则 $\operatorname{D}$ 的纯度越高。根据以上数据,在计算数据集的信息熵时,$\left | y \right |$ 显然只有 man,woman 共 2 种,其中为 man 的概率为 $\frac{8}{17}$, woman 的概率为 $\frac{9}{17}$,则根据公式 $(1)$ 得到数据集的纯度为:
接下来,定义计算信息熵的函数。
import math
def get_Ent(data):
"""
参数:
data -- 数据集
返回:
Ent -- 信息熵
"""
# 计算信息熵
num_sample = len(data) # 样本个数
label_counts = {} # 初始化标签统计字典
for i in range(num_sample):
each_data = data.iloc[i, :]
current_label = each_data["labels"] # 得到当前元素的标签(label)
# 如果标签不在当前字典中,添加该类标签并初始化 value=0,否则该类标签 value+1
if current_label not in label_counts.keys():
label_counts[current_label] = 0
label_counts[current_label] += 1
Ent = 0.0 # 初始化信息熵
for key in label_counts:
prob = float(label_counts[key])/num_sample
Ent -= prob * math.log(prob, 2) # 应用信息熵公式计算信息熵
return Ent
通过计算信息熵函数,计算根节点的信息熵:
base_ent = get_Ent(data)
base_ent
信息增益 就是建立在信息熵的基础上,在离散特征 $x$ 有 $M$ 个取值,如果用 $x$ 对样本 $\operatorname{D}$ 来进行划分,就会产生 $M$ 个分支,其中第 $m$ 个分支包含了集合 $\operatorname{D}$ 的所有在特征 $x$ 上取值为 $m$ 的样本,记为 $\operatorname{D}^{m}$(例如:根据以上生成数据,如果我们用 hair 进行划分,则会产生 long,short 两个分支,每一个分支中分别包含了整个集合中属于 long 或者 short 的数据)。
考虑到不同分支节点包含样本数不同,给分支赋予权重 $\frac{\left | \operatorname{D}^{m}\right |}{\left | \operatorname{D} \right |}$ ,使得样本越多的分支节点影响越大,则 信息增益 的公式就可以得到:
一般情况下,信息增益越大,则说明用 $x$ 来划分样本集合 $\operatorname{D}$ 的纯度越高。以 hair 为例,其中它有 short 和 long 两个可能取值,则分别用 $\operatorname{D}^{1} $(hair = long)和 $\operatorname{D}^{2} $(hair = short)来表示。
其中为 $\operatorname{D}^{1}$ 的数据编号为 ${0,4,6,8,9,10,12,14,15}$ 共 9 个,在这之中为 man 的有 ${0,4,6}$ 共 3 个占比为 $\frac{3}{9}$,为 woman 的有 ${8, 9,10,12,14,15}$ 共 6 个占比为 $\frac{6}{9}$。
同样 $\operatorname{D}^{2}$ 编号为 ${1,2,3,5,7,11,13, 16}$ 共 8 个,其中为 man 的有 ${1,2,3,5,7}$ 共 5 个占比 $\frac{5}{8}$,为 woman 的有 ${11,13, 16}$ 共 3 个占比 $\frac{3}{8}$,若按照 hair 进行划分,则两个分支点的信息熵为:
根据信息增益的公式可以计算出 hair 的信息增益为:
下面我们用 Python 来实现信息增益(ID3)算法:
def get_gain(data, base_ent, feature):
"""
参数:
data -- 数据集
base_ent -- 根节点的信息熵
feature -- 计算信息增益的特征
返回:
Ent -- 信息熵
"""
# 计算信息增益
feature_list = data[feature] # 得到一个特征的全部取值
unique_value = set(feature_list) # 特征取值的类别
feature_ent = 0.0
for each_feature in unique_value:
temp_data = data[data[feature] == each_feature]
weight = len(temp_data)/len(feature_list) # 计算该特征的权重值
temp_ent = weight*get_Ent(temp_data)
feature_ent = feature_ent+temp_ent
gain = base_ent - feature_ent # 信息增益
return gain
完成信息增益函数后,尝试计算特征 hair 的信息增益值。
get_gain(data,base_ent,'hair')
信息增益率(C4.5)
信息增益也存在许多不足之处,经过大量的实验发现,当信息增益作为标准时,易偏向于取值较多的特征,为了避免这种偏好给预测结果带来的不好影响,可以使用增益率来选择最优划分。增益率的公式定义为:
其中:
$\operatorname{IV}(a)$ 称为特征 $a$ 的固有值,当 $a$ 的取值数目越多,则 $\operatorname{IV}(a)$ 的值通常会比较大。例如:
连续值处理
在前面介绍的特征选择中,都是对离散型数据进行处理,但在实际的生活中数据常常会出现连续值的情况,如生成数据中的身高,当数据较少时,可以将每一个值作为一个类别,但当数据量大时,这样是不可取的,在 C4.5 算法中采用二分法对连续值进行处理。
对于连续的属性 $X$ 假设共出现了 $n$ 个不同的取值,将这些取值从小到大排序 ${x_{1},x_{2},x_{3},…,x_{n} } $,其中找一点作为划分点 $t$ ,则将数据划分为两类,大于 $t$ 的为一类,小于 $t$ 的为另一类。而 $t$ 的取值通常为相邻两点的平均数 $t=\frac{x_{i}+x_{i+1}}{2}$。
则在 $n$ 个连续值之中,可以作为划分点的 $t$ 有 $n-1$ 个。通过遍历可以像离散型一样来考察这些划分点。
其中得到样本 $\operatorname{D}$ 基于划分点 $t$ 二分后的信息增益,于是我们可以选择使得 $\operatorname{Gain}(\operatorname{D},X)$ 值最大的划分点。
def get_splitpoint(data, base_ent, feature):
"""
参数:
data -- 数据集
base_ent -- 根节点的信息熵
feature -- 需要划分的连续特征
返回:
final_t -- 连续值最优划分点
"""
# 将连续值进行排序并转化为浮点类型
continues_value = data[feature].sort_values().astype(np.float64)
continues_value = [i for i in continues_value] # 不保留原来的索引
t_set = []
t_ent = {}
# 得到划分点 t 的集合
for i in range(len(continues_value)-1):
temp_t = (continues_value[i]+continues_value[i+1])/2
t_set.append(temp_t)
# 计算最优划分点
for each_t in t_set:
# 将大于划分点的分为一类
temp1_data = data[data[feature].astype(np.float64) > each_t]
# 将小于划分点的分为一类
temp2_data = data[data[feature].astype(np.float64) < each_t]
weight1 = len(temp1_data)/len(data)
weight2 = len(temp2_data)/len(data)
# 计算每个划分点的信息增益
temp_ent = base_ent-weight1 * \
get_Ent(temp1_data)-weight2*get_Ent(temp2_data)
t_ent[each_t] = temp_ent
print("t_ent:", t_ent)
final_t = max(t_ent, key=t_ent.get)
return final_t
实现连续值最优划分点的函数后,寻找 height 连续特征值的划分点。
final_t = get_splitpoint(data, base_ent, 'height')
final_t
决策树算法实现
在对决策树中最佳特征选择和连续值处理之后,接下来就是对决策树的构建。
首先我们将连续值进行处理,在找到最佳划分点之后,将 $
def choice_1(x, t):
if x > t:
return ">{}".format(t)
else:
return "<{}".format(t)
deal_data = data.copy()
# 使用lambda和map函数将 height 按照final_t划分为两个类别
deal_data["height"] = pd.Series(
map(lambda x: choice_1(int(x), final_t), deal_data["height"]))
deal_data
将数据进行预处理之后,接下来就是选择最优的划分特征。
def choose_feature(data):
"""
参数:
data -- 数据集
返回:
best_feature -- 最优的划分特征
"""
# 选择最优划分特征
num_features = len(data.columns) - 1 # 特征数量
base_ent = get_Ent(data)
best_gain = 0.0 # 初始化信息增益
best_feature = data.columns[0]
for i in range(num_features): # 遍历所有特征
temp_gain = get_gain(data, base_ent, data.columns[i]) # 计算信息增益
if (temp_gain > best_gain): # 选择最大的信息增益
best_gain = temp_gain
best_feature = data.columns[i]
return best_feature # 返回最优特征
完成函数之后,我们首先看看数据集中信息增益值最大的特征是什么?
choose_feature(deal_data)
在将所有的子模块构建好之后,最后就是对核心决策树的构建,这篇文章采用信息增益(ID3)的方式构建决策树。在构建的过程中,根据算法流程,我们反复遍历数据集,计算每一个特征的信息增益,通过比较将最好的特征作为父节点,根据特征的值确定分支子节点,然后重复以上操作,直到某一个分支全部属于同一类别,或者遍历完所有的数据特征,当遍历到最后一个特征时,若分支数据依然「不纯」,就将其中数量较多的类别作为子节点。
因此最好采用递归的方式来构建决策树。
def create_tree(data):
"""
参数:
data -- 数据集
返回:
tree -- 以字典的形式返回决策树
"""
# 构建决策树
feature_list = data.columns[:-1].tolist()
label_list = data.iloc[:, -1]
if len(data["labels"].value_counts()) == 1:
leaf_node = data["labels"].mode().values
return leaf_node # 第一个递归结束条件:所有的类标签完全相同
if len(feature_list) == 1:
leaf_node = data["labels"].mode().values
return leaf_node # 第二个递归结束条件:用完了所有特征
best_feature = choose_feature(data) # 最优划分特征
tree = {best_feature: {}}
feat_values = data[best_feature]
unique_value = set(feat_values)
for value in unique_value:
temp_data = data[data[best_feature] == value]
temp_data = temp_data.drop([best_feature], axis=1)
tree[best_feature][value] = create_tree(temp_data)
return tree
完成创建决策树函数后,接下来对我们第一棵树进行创建。
tree = create_tree(deal_data)
tree
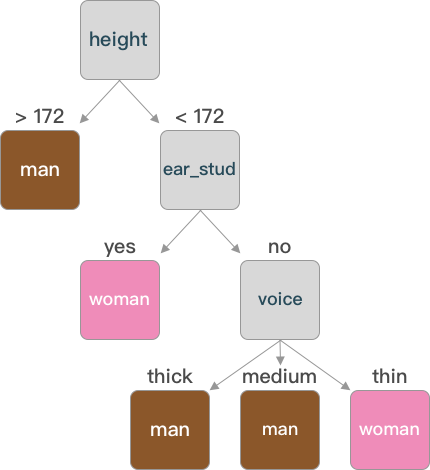
通过字典的方式表示构建好的树,可以通过图像的方式更加直观的了解。
通过图形可以看出,在构建决策树时不一定每一个特征都会成为树的节点(如同 hair)。
在构建好决策树之后,最终就可以使用未知样本进行预测分类。
def classify(tree, test):
"""
参数:
data -- 数据集
test -- 需要测试的数据
返回:
class_label -- 分类结果
"""
# 决策分类
first_feature = list(tree.keys())[0] # 获取根节点
feature_dict = tree[first_feature] # 根节点下的树
labels = test.columns.tolist()
value = test[first_feature][0]
for key in feature_dict.keys():
if value == key:
if type(feature_dict[key]).__name__ == 'dict': # 判断该节点是否为叶节点
class_label = classify(feature_dict[key], test) # 采用递归直到遍历到叶节点
else:
class_label = feature_dict[key]
return class_label
在分类函数完成之后,接下来我们尝试对未知数据进行分类。
test = pd.DataFrame({"hair": ["long"], "voice": ["thin"], "height": [163], "ear_stud": ["yes"]})
test
对连续值进行预处理:
test["height"] = pd.Series(map(lambda x: choice_1(int(x), final_t), test["height"]))
test
分类预测:
classify(tree,test)
一个身高 163 厘米,长发,带着耳钉且声音纤细的人,在我们构建的决策树判断后预测为一名女性。
上面的文章中,我们没有考虑 $=划分点$ 的情况,你可以自行尝试将 $>=划分点$ 或 $<=划分点$ 归为一类,看看结果又有哪些不同?
预剪枝和后剪枝
在决策树的构建过程中,特别在数据特征非常多时,为了尽可能正确的划分每一个训练样本,结点的划分就会不停的重复,则一棵决策树的分支就非常多。对于训练集而言,拟合出来的模型是非常完美的。但是,这种完美就使得整体模型的复杂度变高,同时对其他数据集的预测能力下降,也就是我们常说的过拟合使得模型的泛化能力变弱。为了避免过拟合问题的出现,在决策树中最常见的两种方法就是预剪枝和后剪枝。
预剪枝
预剪枝,顾名思义预先减去枝叶,在构建决策树模型的时候,每一次对数据划分之前进行估计,如果当前节点的划分不能带来决策树泛化的提升,则停止划分并将当前节点标记为叶节点。例如前面构造的决策树,按照决策树的构建原则,通过 height 特征进行划分后 $<172$ 分支中又按照 ear_stud 特征值进行继续划分。如果应用预剪枝,则当通过 height 进行特征划分之后,对 $<172$ 分支是否进行 ear_stud 特征进行划分时计算划分前后的准确度,如果划分后的更高则按照 ear_stud 继续划分,如果更低则停止划分。
后剪枝
跟预剪枝在构建决策树的过程中判断是否继续特征划分所不同的是,后剪枝在决策树构建好之后对树进行修剪。如果说预剪枝是自顶向下的修剪,那么后剪枝就是自底向上进行修剪。后剪枝将最后的分支节点替换为叶节点,判断是否带来决策树泛化的提升,是则进行修剪,并将该分支节点替换为叶节点,否则不进行修剪。例如在前面构建好决策树之后,$>172$分支的 voice 特征,将其替换为叶节点如(man),计算替换前后划分准确度,如果替换后准确度更高则进行修剪(用叶节点替换分支节点),否则不修剪。
学生成绩分类预测
在前面我们使用 Python 将决策树的特征选择,连续值处理和预测分类做了详细的讲解。接下来我们应用决策树模型对真实的数据进行分类预测。
本次应用到的数据为学生成绩数据集 course-13-student.csv,一共有 395 条数据,26 个特征。首先加载并预览数据集:
# 导入数据集并预览
stu_grade = pd.read_csv('https://labfile.oss.aliyuncs.com/courses/1081/course-13-student.csv')
stu_grade.head()
由于特征过多,我们选择部分特征作为决策树模型的分类特征,分别为:
- school:学生所读学校(GP,MS)
- sex:性别(F:女,M:男)
- address:家庭住址(U:城市,R:郊区)
- Pstatus:父母状态(A:同居,T:分居)
- Pedu:父母学历由低到高
- reason:选择这所学校的原因(home:家庭,course:课程设计,reputation:学校地位,other:其他)
- guardian:监护人(mother:母亲,father:父亲,other:其他)
- studytime:周末学习时长
- schoolsup:额外教育支持(yes:有,no:没有)
- famsup:家庭教育支持(yes:有,no:没有)
- paid:是否上补习班(yes:是,no:否)
- higher:是否想受更好的教育(yes:是,no:否)
- internet:是否家里联网(yes:是,no:否)
- G1:一阶段测试成绩
- G2:二阶段测试成绩
- G3:最终成绩
new_data = stu_grade.iloc[:, [0, 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 14, 15, 24, 25, 26]]
new_data.head()
首先我们将成绩 G1,G2,G3 根据分数进行等级划分,将 0-4 划分为 bad,5-9 划分为 medium ,
def choice_2(x):
x = int(x)
if x < 5:
return "bad"
elif x >= 5 and x < 10:
return "medium"
elif x >= 10 and x < 15:
return "good"
else:
return "excellent"
stu_data = new_data.copy()
stu_data["G1"] = pd.Series(map(lambda x: choice_2(x), stu_data["G1"]))
stu_data["G2"] = pd.Series(map(lambda x: choice_2(x), stu_data["G2"]))
stu_data["G3"] = pd.Series(map(lambda x: choice_2(x), stu_data["G3"]))
stu_data.head()
同样我们对 Pedu(父母教育程度)也进行划分
def choice_3(x):
x = int(x)
if x > 3:
return "high"
elif x > 1.5:
return "medium"
else:
return "low"
stu_data["Pedu"] = pd.Series(map(lambda x: choice_3(x), stu_data["Pedu"]))
stu_data.head()
在等级划分之后,为遵循 scikit-learn 函数的输入规范,需要将数据特征进行替换。
def replace_feature(data):
"""
参数:
data -- 数据集
返回:
data -- 将特征值替换后的数据集
"""
# 特征值替换
for each in data.columns: # 遍历每一个特征名称
feature_list = data[each]
unique_value = set(feature_list)
i = 0
for fea_value in unique_value:
data[each] = data[each].replace(fea_value, i)
i += 1
return data
将特征值进行替换后展示。
stu_data = replace_feature(stu_data)
stu_data.head()
加载好预处理的数据集之后,为了实现决策树算法,同样我们需要将数据集分为 训练集和测试集,依照经验:训练集占比为 70%,测试集占 30%。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(stu_data.iloc[:, :-1], stu_data["G3"],
test_size=0.3, random_state=5)
X_test.head()
在划分好数据集之后,接下来就是进行预测。在前面的文章中我们采用 Python 对决策树算法进行实现,下面我们通过 scikit-learn 来对其进行实现。 scikit-learn 决策树类 DecisionTreeClassifier(criterion='gini', random_state=None) 常用参数如下:
criterion表示特征划分方法选择,默认为 gini (在后面会讲到),可选择为 entropy (信息增益)。ramdom_state表示随机数种子,当特征特别多时 scikit-learn 为了提高效率,随机选取部分特征来进行特征选择,即找到所有特征中较优的特征。
from sklearn.tree import DecisionTreeClassifier
dt_model = DecisionTreeClassifier(criterion='entropy', random_state=34)
dt_model.fit(X_train,y_train) # 使用训练集训练模型
决策树可视化
在构建好决策树之后,我们需要对创建好的决策树进行可视化展示,引入 export_graphviz 进行画图。
下面开始生成决策树图像,其中生成决策树较大需要拖动滑动条进行查看。
pip install graphviz # 安装 graphviz 可视化库
from sklearn.tree import export_graphviz
import graphviz
img = export_graphviz(
dt_model, out_file=None,
feature_names=stu_data.columns[:-1].values.tolist(), # 传入特征名称
class_names=np.array(["bad", "medium", "good", "excellent"]), # 传入类别值
filled=True, node_ids=True,
rounded=True)
graphviz.Source(img) # 展示决策树
y_pred = dt_model.predict(X_test) # 使用模型对测试集进行预测
y_pred
from sklearn.metrics import accuracy_score
# 计算分类准确度
accuracy_score(y_test, y_pred)
CART 决策树
分类与回归树(classification and regression tree, CART)同样也是应用广泛的决策树学习算法,CART 算法是按照特征划分,由树的生成和树的剪枝构成,既可以进行分类又可以用于回归,按照作用将其分为决策树和回归树,由于这篇文章设计为决策树的概念,所以回归树的部分有兴趣的同学可以自己查找相关资料进一步学习。
CART 决策树的构建和常见的 ID3 和 C4.5 算法的流程相似,但在特征划分选择上 CART 选择了 基尼指数 作为划分标准。数据集 $\operatorname{D}$ 的纯度可用基尼值来度量:
基尼指数表示随机抽取两个样本,两个样本类别不一致的概率,基尼指数越小则数据集的纯度越高。同样对于每一个特征值的基尼指数计算,其和 ID3 、 C4.5 相似,定义为:
在进行特征划分的时候,选择特征中基尼值最小的作为最优特征划分点。
实际上,在应用过程中,更多的会使用 基尼指数 对特征划分点进行决策,最重要的原因是计算复杂度相较于 ID3 和 C4.5 小很多(没有对数运算)。
小结
这篇文章中学习了决策树的原理和算法流程,采用数学公式和实际例子相结合的方式讲解了信息增益和增益率的特征划分方法。通过 Python 代码对决策树进行完整实现,并且使用 scikit-learn 对实际数据应用决策树进行分类预测。
相关链接
系列文章
- 综述及示例
- 线性回归实现与应用
- 多项式回归实现与应用
- 岭回归和 LASSO 回归实现
- 回归模型评价与检验
- 逻辑回归实现与应用
- K-近邻算法实现与应用
- 朴素贝叶斯实现及应用
- 分类模型评价方法
- 支持向量机实现与应用
- 决策树实现与应用
- 装袋和提升集成学习方法
- 划分聚类方法实现与应用
- 层次聚类方法实现与应用
- 主成分分析原理及应用
- 密度聚类方法实现与应用
- 谱聚类及其他聚类方法应用
- 自动化机器学习综述
- 自动化机器学习实践应用
- 模型动态增量训练
- 模型推理与部署
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️