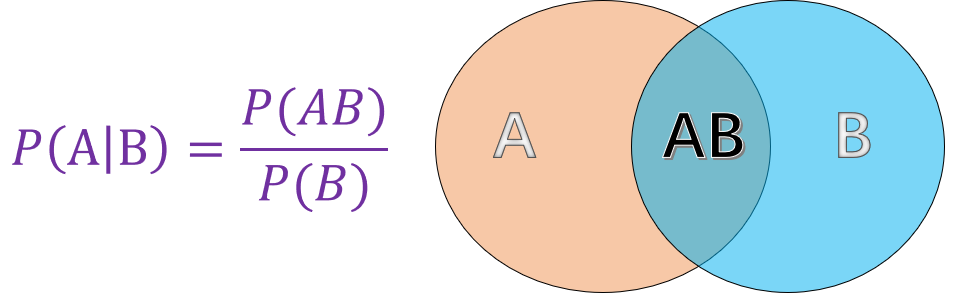介绍

在分类预测中，以概率论作为基础的算法比较少，而朴素贝叶斯就是其中之一。朴素贝叶斯算法实现简单，且预测分类的效率很高，是一种十分常用的算法。这篇文章主要从贝叶斯定理和参数估计两个方面讲解朴素贝叶斯算法的原理并结合数据进行实现，最后通过一个例子进行实战练习。

知识点

• 条件概率
• 贝叶斯定理
• 朴素贝叶斯原理
• 朴素贝叶斯算法实现
• 极大似然估计

基本概念

朴素贝叶斯的数学理论基础源于概率论。所以，在学习朴素贝叶斯算法之前，首先对这篇文章中涉及到的概率论知识做简要讲解。

条件概率

条件概率就是指事件 $A$ 在另外一个事件 $B$ 已经发生条件下的概率。如图所示：

其中：

• $P(A)$ 表示 $A$ 事件发生的概率。
• $P(B)$ 表示 $B$ 事件发生的概率。
• $P(AB)$ 表示 $A, B$ 事件同时发生的概率。

而最终计算得到的 $P(A \mid B)$ 便是条件概率，表示在 $B$ 事件发生的情况下 $A$ 事件发生的概率。

贝叶斯定理

上面提到了条件概率的基本概念，那么当知道事件 $B$ 发生的情况下事件 $A$ 发生的概率 $P(A \mid B)$ ，如何求 $P(B \mid A)$ 呢？贝叶斯定理应运而生。根据条件概率公式可以得到:

而同样通过条件概率公式可以得到：

将 $(2)$ 式带入 $(1)$ 式便可得到完整的贝叶斯定理：

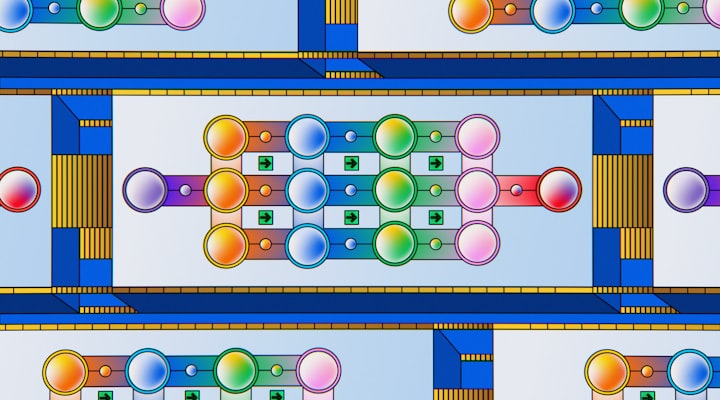
以下，通过一张图来完整且形象的展示条件概率和贝叶斯定理的原理。

先验概率

先验概率（Prior Probability）指的是根据以往经验和分析得到的概率。例如以上公式中的 $P(A), P(B)$ ,又例如：$X$ 表示投一枚质地均匀的硬币，正面朝上的概率，显然在我们根据以往的经验下，我们会认为 $X$ 的概率 $P(X) = 0.5$ 。其中 $P(X) = 0.5$ 就是先验概率。

后验概率

后验概率（Posterior Probability）是事件发生后求的反向条件概率；即基于先验概率通过贝叶斯公式求得的反向条件概率。例如公式中的 $P(B \mid A)$ 就是通过先验概率 $P(A)$ 和$P(B)$ 得到的后验概率，其通俗的讲就是「执果寻因」中的「因」。

朴素贝叶斯原理

朴素贝叶斯（Naive Bayes）就是将贝叶斯原理以及条件独立结合而成的算法，其思想非常的简单，根据贝叶斯公式：

变形表达式为：

公式 $(5)$ 利用先验概率，即特征和类别的概率；再利用不同类别中各个特征的概率分布，最后计算得到后验概率，即各个特征分布下的预测不同的类别。

利用贝叶斯原理求解固然是一个很好的方法，但实际生活中数据的特征之间是有相互联系的，在计算 $P(\text{特征} \mid \text{类别})$ 时，考虑特征之间的联系会比较麻烦，而朴素贝叶斯则人为的将各个特征割裂开，认定特征之间相互独立。

朴素贝叶斯中的「朴素」，即条件独立，表示其假设预测的各个属性都是相互独立的,每个属性独立地对分类结果产生影响，条件独立在数学上的表示为：$P(AB)=P(A) \times P(B)$ 。这样，使得朴素贝叶斯算法变得简单，但有时会牺牲一定的分类准确率。对于预测数据，求解在该预测数据的属性出现时各个类别的出现概率，将概率值大的类别作为预测数据的类别。

关于贝叶斯定理和朴素贝叶斯方法，这里有一个有趣的视频，希望能帮助大家加深理解。

朴素贝叶斯算法实现

前面主要介绍了朴素贝叶斯算法中几个重要的概率论知识，接下来我们对其进行具体的实现，算法流程如下：

• 第 1 步：设 $X = \left { a_{1},a_{2},a_{3},…,a_{n} \right }$ 为预测数据，其中 $a_{i}$ 是预测数据的特征值。
• 第 2 步：设 $Y = \left {y_{1},y_{2},y_{3},…,y_{m} \right }$ 为类别集合。
• 第 3 步：计算 $P(y_{1}\mid x)$ , $P(y_{2}\mid x)$ , $P(y_{3}\mid x)$ , $…$, $P(y_{m}\mid x)$ 。
• 第 4 步：寻找 $P(y_{1}\mid x)$ , $P(y_{2}\mid x)$ , $P(y_{3}\mid x)$ , $…$, $P(y_{m}\mid x)$ 中最大的概率 $P(y_{k}\mid x)$ ，则 $x$ 属于类别 $y_{k}$。

下面我们利用 Python 完成一个朴素贝叶斯算法的分类。首先生成一组示例数据：由 $A$ 和 $B$ 两个类别组成，每个类别包含 $x$，$y$ 两个特征值，其中 $x$ 特征包含 $r, g, b$（红，绿，蓝）三个类别，$y$ 特征包含 $s, m, l$（小，中，大）三个类别，如同数据 $X = [g,l]$。

import pandas as pd


def create_data():
    # 生成示例数据
    data = {"x": ['r', 'g', 'r', 'b', 'g', 'g', 'r', 'r', 'b', 'g', 'g', 'r', 'b', 'b', 'g'],
            "y": ['m', 's', 'l', 's', 'm', 's', 'm', 's', 'm', 'l', 'l', 's', 'm', 'm', 'l'],
            "labels": ['A', 'A', 'A', 'A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B', 'B', 'B']}
    data = pd.DataFrame(data, columns=["labels", "x", "y"])
    return data

在创建好数据后，接下来进行加载数据，并进行预览。

data = create_data()
data

参数估计

根据朴素贝叶斯的原理，最终分类的决策因素是比较 $\left { P(\text{类别 1} \mid \text{特征}),P(\text{类别 2} \mid \text{特征}),…,P(\text{类别} m \mid \text{特征}) \right }$ 各个概率的大小，根据贝叶斯公式得知每一个概率计算的分母 $P(\text{特征})$ 都是相同的，只需要比较分子 $P(\text{类别})$ 和 $P(\text{特征} \mid \text{类别})$ 乘积的大小。

那么如何得到 $P(\text{类别})$ ,以及 $P(\text{特征} \mid \text{类别})$ 呢？在概率论中，可以应用极大似然估计法以及贝叶斯估计法来估计相应的概率。

极大似然估计

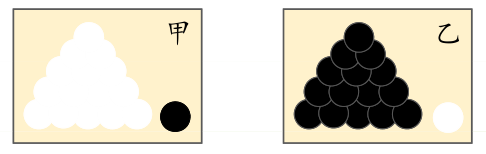
什么是极大似然？下面通过一个简单的例子让你有一个形象的了解：

前提条件：假如有两个外形完全相同箱子，甲箱中有 99 个白球，1 个黑球；乙箱中有 99 个黑球，1 个白球。

问题：当我们进行一次实验，并取出一个球，取出的结果是白球。那么，请问白球是从哪一个箱子里取出的？

我相信，你的第一印象很可能会是白球从甲箱中取出。因为甲箱中的白球数量多，所以这个推断符合人们经验。其中「最可能」就是「极大似然」。而极大似然估计的目的就是利用已知样本结果，反推最有可能造成这个结果的参数值。

极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：「模型已定，参数未知」。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

在概率论中求解极大似然估计的方法比较复杂，我们将讲解 $P(B)$ 和 $P(B/A)$ 是如何通过极大似然估计得到的。$P(\text{种类})$ 用数学的方法表示 ：

公式 $(6)$ 中的 $y_{i}$ 表示数据的类别，$c_{k}$ 表示每一条数据的类别。

你可以通俗的理解为，在现有的训练集中，每一个类别所占总数的比例，例如:生成的数据中 $P(Y=A)=\frac{8}{15}$，表示训练集中总共有 15 条数据，而类别为 $A$ 的有 8 条数据。

下面我们用 Python 代码来实现先验概率 $P(\text{种类})$ 的求解：

def get_P_labels(labels):
    # P(\text{种类}) 先验概率计算
    labels = list(labels)  # 转换为 list 类型
    P_label = {}  # 设置空字典用于存入 label 的概率
    for label in labels:
        # 统计 label 标签在标签集中出现的次数再除以总长度
        P_label[label] = labels.count(
            label) / float(len(labels))  # p = count(y) / count(Y)
    return P_label


P_labels = get_P_labels(data["labels"])
P_labels

$P(\text{特征} \mid \text{种类})$ 由于公式较为繁琐这里先不给出，直接用叙述的方式能更清晰地帮助理解：

实际需要求的先验估计是特征的每一个类别对应的每一个种类的概率，例如：生成数据中 $P(x_{1}=r \mid Y=A)=\frac{4}{8}$， $A$ 的数据有 8 条，而在种类为 $A$ 的数据且特征 $x$ 为 $r$ 的有 4 条。

同样我们用代码将先验概率 $P(\text{特征} \mid \text{种类})$ 实现求解，首先我们将特征按序号合并生成一个 NumPy 数组。

import numpy as np

# 将 data 中的属性切割出来，即 x 和 y 属性
train_data = np.array(data.iloc[:, 1:])
train_data

在寻找属于某一类的某一个特征时，我们采用对比索引的方式来完成。开始得到每一个类别的索引：

labels = data["labels"]
label_index = []
# 遍历所有的标签，这里就是将标签为 A 和 B 的数据集分开，label_index 中存的是该数据的下标
for y in P_labels.keys():
    temp_index = []
    # enumerate 函数返回 Series 类型数的索引和值，其中 i 为索引，label 为值
    for i, label in enumerate(labels):
        if (label == y):
            temp_index.append(i)
        else:
            pass
    label_index.append(temp_index)
label_index

得到 $A$ 和 $B$ 的索引，其中是 $A$ 类别为前 $8$ 条数据，$B$ 类别为后 $7$ 条数据。

在得到类别的索引之后，接下来就是找到我们需要的特征为 $r$ 的索引值。

# 遍历 train_data 中的第一列数据，提取出里面内容为r的数据
x_index = [i for i, feature in enumerate(
    train_data[:, 0]) if feature == 'r']  # 效果等同于求类别索引中 for 循环

x_index

得到的结果为 $x$ 特征值为 $r$ 的数据索引值。

最后通过对比类别为 $A$ 的索引值，计算出既符合 $x = r$ 又符合 $A$ 类别的数据在 $A$ 类别中所占比例。

# 取集合 x_index （x 属性为 r 的数据集合）与集合 label_index[0]（标签为 A 的数据集合）的交集
x_label = set(x_index) & set(label_index[0])
print('既符合 x = r 又是 A 类别的索引值：', x_label)
x_label_count = len(x_label)
# 这里就是用类别 A 中的属性 x 为 r 的数据个数除以类别 A 的总个数
print('先验概率 P(r|A):', x_label_count / float(len(label_index[0])))  # 先验概率的计算公式

为了方便后面函数调用，我们将求 $P(\text{特征}\mid \text{种类})$ 代码整合为一个函数。

def get_P_fea_lab(P_label, features, data):
    # P(\text{特征}∣种类) 先验概率计算
    # 该函数就是求 种类为 P_label 条件下特征为 features 的概率
    P_fea_lab = {}
    train_data = data.iloc[:, 1:]
    train_data = np.array(train_data)
    labels = data["labels"]
    # 遍历所有的标签
    for each_label in P_label.keys():
        # 上面代码的另一种写法，这里就是将标签为 A 和 B 的数据集分开，label_index 中存的是该数据的下标
        label_index = [i for i, label in enumerate(
            labels) if label == each_label]

        # 遍历该属性下的所有取值
        # 求出每种标签下，该属性取每种值的概率
        for j in range(len(features)):
            # 筛选出该属性下属性值为 features[j] 的数据
            feature_index = [i for i, feature in enumerate(
                train_data[:, j]) if feature == features[j]]

            # set(x_index)&set(y_index) 取交集，得到标签值为 each_label,属性值为 features[j] 的数据集合
            fea_lab_count = len(set(feature_index) & set(label_index))
            key = str(features[j]) + '|' + str(each_label)  # 拼接字符串

            # 计算先验概率
            # 计算 labels 为 each_label下，featurs 为 features[j] 的概率值
            P_fea_lab[key] = fea_lab_count / float(len(label_index))
    return P_fea_lab


features = ['r', 'm']
get_P_fea_lab(P_labels, features, data)

可以得到当特征 $x$ 和 $y$ 的值为 $r$ 和 $m$ 时，在不同类别下的先验概率。

贝叶斯估计

在做极大似然估计时，若类别中缺少一些特征，则就会出现概率值为 0 的情况。此时，就会影响后验概率的计算结果，使得分类产生偏差。而解决这一问题最好的方法就是采用贝叶斯估计。

在计算先验概率 $P(\text{种类})$ 中，贝叶斯估计的数学表达式为：

其中 $\lambda \geq 0$ 等价于在随机变量各个取值的频数上赋予一个正数，当 $\lambda=0$ 时就是极大似然估计。在平时常取 $\lambda=1$，这时称为拉普拉斯平滑。例如：生成数据中，$P(Y=A)=\frac{8+1}{15+2*1}=\frac{9}{17}$，取 $\lambda=1$ 此时由于一共有 $A$，$B$ 两个类别，则 $k$ 取 2。

同样计算 $P(\text{特征} \mid \text{种类})$ 时，也是给计算时的分子分母加上拉普拉斯平滑。例如：生成数据中，$P(x_{1}=r \mid Y=A)=\frac{4+1}{8+3*1}=\frac{5}{11}$ 同样取 $\lambda=1$ 此时由于 $x$ 中有 $r$, $g$, $b$ 三个种类，所以这里 k 取值为 3。

通过上面的内容，相信你已经对朴素贝叶斯算法原理有一定印象。接下来，我们对朴素贝叶斯分类过程进行完整实现。其中，参数估计方法则使用极大似然估计。

def classify(data, features):
    # 朴素贝叶斯分类器
    # 求 labels 中每个 label 的先验概率
    labels = data['labels']
    # 这里也就是求 P（B），P_label 为一个字典，存的是每个 B 对应的 P(B)
    P_label = get_P_labels(labels)
    P_fea_lab = get_P_fea_lab(P_label, features, data)  # 这里是在求 P（A|B）

    P = {}
    P_show = {}  # 后验概率
    for each_label in P_label:
        P[each_label] = P_label[each_label]
        # 遍历每个标签下的每种属性
        for each_feature in features:
            # 拼接字符串为 P(B/A) 用于字典的键值
            key = str(each_label)+'|'+str(features)
            # 计算 P(B/A) = P(B) * P(A/B) 因为所有的后验概率，分母相同。因此，在计算时可以忽略掉。
            P_show[key] = P[each_label] * \
                P_fea_lab[str(each_feature) + '|' + str(each_label)]
            # 把刚才算的概率放到 P 列表里面，这个 P 列表的键值变成了标签。
            # 这样做的目的，其实是为了在后面取最大时，取出就是标签，而不是 标签|特征
            P[each_label] = P[each_label] * \
                P_fea_lab[str(each_feature) + '|' +
                          str(each_label)]
    # 输出 P_show 和 P 观察，发现他们的概率值没有变，只是字典的 key 值变了
    print(P_show)
    print(P)
    features_label = max(P, key=P.get)  # 概率最大值对应的类别
    return features_label

classify(data, ['r', 'm'])

对于特征为 $[r,m]$ 的数据通过朴素贝叶斯分类得到不同类别的概率值，经过比较后分为 $A$ 类。

朴素贝叶斯的三种常见模型

了解完朴素贝叶斯算法原理后，在实际数据中，我们可以依照特征的数据类型不同，在计算先验概率方面对朴素贝叶斯模型进行划分，并分为：多项式模型，伯努利模型和高斯模型。

多项式模型

当特征值为离散时，常常使用多项式模型。事实上，在以上参数估计中，我们所应用的就是多项式模型。为避免概率值为 0 的情况出现，多项式模型采用的是贝叶斯估计。

伯努利模型

与多项式模型一样，伯努利模型适用于离散特征的情况，所不同的是，伯努利模型中每个特征的取值只能是 1 和 0（以文本分类为例，某个单词在文档中出现过，则其特征值为 1，否则为 0）。

在伯努利模型中，条件概率 $P(x_{i} \mid y_{k})$ 的计算方式为：

• 当特征值 $x_{i}=1$ 时，$P(x_{i} \mid y_{k})=P(x_{i}=1 \mid y_{k})$ ;
• 当特征值 $x_{i}=0$ 时，$P(x_{i} \mid y_{k})=P(x_{i}=0 \mid y_{k})$ 。

高斯模型

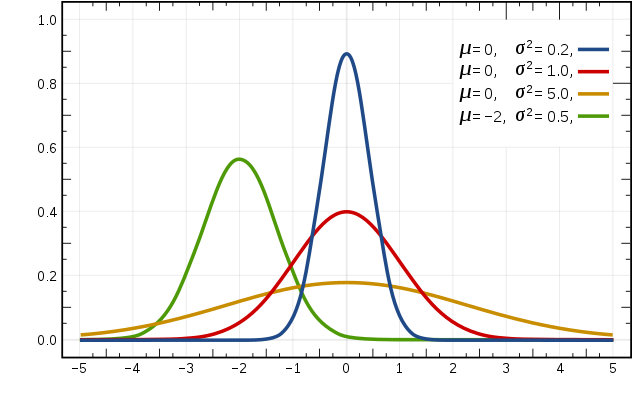
当特征是连续变量的时候，在不做平滑的情况下，运用多项式模型就会导致很多 $P(x_{i} \mid y_{k})=0$，此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，采用高斯模型。高斯模型是假设连续变量的特征数据是服从高斯分布的，高斯分布函数表达式为：

其中：

• $\mu_{y_{k},i}$ 表示类别为 $y_{k}$ 的样本中，第 $i$ 维特征的均值。
• $\sigma ^{2}_{y_{k}},i$ 表示类别为 $y_{k}$ 的样本中，第 $i$ 维特征的方差。

高斯分布示意图如下：

朴素贝叶斯垃圾邮件分类

接下来，我们应用朴素贝叶斯算法模型对真实数据进行分类预测。垃圾邮件过滤（spam filtering）是机器学习中一个非常经典的问题，其涉及到将电子邮件分为垃圾邮件（spam）或正常邮件（ham）的操作。你的 Gmail 账户的垃圾邮箱就是最好的例子。

数据集介绍及预处理

首先先了解一下这篇文章使用到的数据集: trec06c。

trec06c 是一个公开的垃圾邮件语料库，由国际文本检索会议提供，分为英文数据集（trec06p）和中文数据集（trec06c），其中所含的邮件均来源于真实邮件保留了邮件的原有格式和内容。

你可以前往 2006 TREC Public Spam Corpora 下载 trec06c.tgz 这个文件，也可以使用提供的链接下载:

wget -nc "https://labfile.oss.aliyuncs.com/courses/1176/trec06c.zip"  # 下载数据
!unzip -o trec06c.zip

接下来，我们使用 read_table 加载数据集。

data = pd.read_table('trec06c/full/index', header=None,
                     encoding='gb2312', delim_whitespace=True)
data.head()

读取完成之后，可以看到整个数据集一共有 64620 个样本，第一列代表的是是否是垃圾邮件，标记 spam 是垃圾邮件，标记 ham 是正常邮件。第二列则是邮件内容的文本文件的路径。

接下来用 0 替代 spam，1 替代 ham，然后替换掉文件路径。为了加速运算，这篇文章只使用 1 万条样本数据。

df = data.replace(['spam', 'ham'], [0, 1])  # 0 替代 spam，1 替代 ham
df = df.replace(regex=["\.."], value='trec06c')  # 替换掉文件路径
df = df.sample(len(df), random_state=1, )[:10000]  # 打乱样本并取前 1 万条数据
df.groupby(0).count()  # 统计样本

统计样本量之后，垃圾邮件有 6595 个，正常邮件有 3405 个。

你可以使用 shell 命令输出一封垃圾邮件内容，不过需要转换编码才能正常显示中文。

cat "trec06c/data/000/002" | iconv -f GBK -t UTF-8  # 显示文件内容并转为 UTF-8 编码

邮件由两部分组成，第一部分包含了邮件的信息，例如发件人，标题等等，第二部分才是邮件正文。这些文件不是 UTF-8 编码的，所以需要将其转为 UTF-8 编码。

由于本次试验会用到的只有邮件正文内容，所以需要去除第一部分，另外正文部分还有许多链接等其他不需要的内容。因此，所以我们需要对原始数据做一些数据预处理，包括以下几个内容。

1. 转换源数据编码格式为 UTF-8 格式。
2. 过滤字符：去除所有非中文字符，如标点符号、英文字符、数字、网站链接等特殊字符。
3. 过滤停用词。
4. 对邮件内容进行分词处理。

数据清洗的步骤中，首先通过正则表达式滤掉了所有英文，数字，标点符号，特殊符号，最后只保留了汉字。与此同时，内容里还存在一些长相奇怪的文字，我们通过 Unicode 中文编码范围 0x4e00-0x9fff 过滤。

import re

def clean_str(line):
    # 清理邮件，替换不需要的字符串
    line.strip('\n')
    line = re.sub(r"[^\u4e00-\u9fff]", "", line)
    line = re.sub(
        "[0-9a-zA-Z\-\s+\.\!\/_,$%^*\(\)\+(+\"\')]+|[+——！，。？、~@#￥%……&*（）<>\[\]:：★◆【】《》;；=?？]+", "", line)
    return line.strip()

完成对邮件文本的初步清理后，接下来需要对文本进行分词。文章中，我们使用到了非常著名的 结巴分词 模块。

在中文中，有很多的非实意词语或者其他并没有实际作用的词语，这些词语必须在分词之后进行过滤，这个环节也就是过滤停用词。通过下载一个预先设定的停用词表，然后判断是否是停用词来过滤分词结果。这里提供一个比较全的 stopwords.txt 文件，需要下载之后才能使用。另外如果是空行，则需要剔除。分词之后需剔除只有一个字的结果全部，这一点很容易理解，因为一个字基本上没有什么内容。

# 下载停用词表
wget -nc "https://labfile.oss.aliyuncs.com/courses/1176/stopwords.txt"

然后，按照上面陈述的逻辑，编写分词与过滤停用词函数。

def load_stopwords(file_path):
    # 加载停用词
    with open(file_path, 'r') as f:
        stopwords = [line.strip('\n') for line in f.readlines()]
    return stopwords

stopwords = load_stopwords('stopwords.txt')
stopwords

import jieba

def process(file_path, test_mode=False):
    # 清洗一封邮件
    '''
    - file_path: 文本文件路径
    - test_mode: 测试模式，后文我们会将一个字符串写入文件(utf-8 编码)，而训练文件以 GBK 编码，
                 如果自己实现分类，请注意编码格式，通常为 utf-8
    - return: words, 处理、分词之后的有效词语
    '''
    words = []
    with open(file_path, 'rb') as f:
        for line in f.readlines():
            if not test_mode:
                line = line.strip().decode("gbk", 'ignore')
            else:
                line = line.strip().decode("utf-8", 'ignore')
            line = clean_str(line)
            if len(line) == 0:
                continue
            seg_list = list(jieba.cut(line, cut_all=False))
            for x in seg_list:
                if len(x) <= 1:
                    continue
                if x in stopwords:
                    continue
                words.append(x)
    return words

接下来，我们尝试对 trec06c/data/000/000 垃圾邮件执行分词和过滤停用词操作。

words = process('trec06c/data/000/000')
" ".join(words)

然后，我们需要对全部样本进行分词操作。由于此过程执行时间较长，这里使用 tqdm 模块显示处理进度。

from tqdm import tqdm

tqdm.pandas()  # 使用 tqdm 显示进度
# 将 apply 函数替换为 progress_apply 以使用 tqdm 显示处理进度
df['words'] = df[1].progress_apply(process)
df.head()

分词结束之后，我们需要对分词结果进一步处理。由于文字无法直接被算法理解，所以这里就需要把分词结果编码为可以输入算法的向量。这里，我们会用到自然语言领域常用的 Word2vec 方法。该方法由 Google 创造，可以阅读 Word2vec-维基百科。

由于 Google 仅提供了 C 版本的 Word2vec 方法，实验使用 gensim 提供的 Word2vec API。此过程执行时间较长，请耐心等待。

from gensim.models import Word2Vec
from tqdm import tqdm_notebook

# 移除一些不必要的警告
import warnings
warnings.filterwarnings('ignore')

# 导入上面保存的分词数组
data = df['words']

# 训练 Word2Vec 浅层神经网络模型
w2v_model = Word2Vec(size=100, min_count=10)
w2v_model.build_vocab(data)
w2v_model.train(data, total_examples=w2v_model.corpus_count, epochs=5)
w2v_model

def sum_vec(text):
    # 对每个句子的进行词向量求和计算
    vec = np.zeros(100).reshape((1, 100))
    for word in text:
        try:
            # 得到句子中每个词的词向量并累加在一起
            vec += w2v_model[word].reshape((1, 100))
        except KeyError:
            continue
    return vec

# 将词向量保存为 Ndarray
data_vec = np.concatenate([sum_vec(z) for z in tqdm_notebook(data)])
data_vec.shape

代码中我们初始化了一个 $(1,100)$ 全为 0 的向量充当容器，循环遍历一篇文章 text 通过 w2v_model[i] 输出每个词 i 在已经训练好了的模型 w2v_model 中的向量表示，然后通过对每个词的向量表示使用 vec 进行累计得到该文章 text 整体的向量表示。

你会发现，邮件分词结果就被转换为了向量。 $(10000, 100)$ 表示有 10000 条样本，邮件内容被编码为指定 100 长度的向量。

接下来，就可以开始划分数据并使用朴素贝叶斯建模了。

数据划分及建模

数据预处理之后，我们同样需要将数据集分为 训练集和测试集，依照经验：训练集占比为 80%，测试集占 20%。在此，同样使用 scikit-learn 模块的 train_test_split 函数完成数据集切分。

from sklearn.model_selection import train_test_split

feature_data = data_vec
label_data = df[0].values
# 分割数据
X_train, X_test, y_train, y_test = train_test_split(
    feature_data, label_data, test_size=0.2, random_state=4)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

前面的文章中我们采用 Python 对朴素贝叶斯算法进行实现，下面我们通过 scikit-learn 来对其进行实现。由于 scikit-learn 中的多项式模型规定传入的矩阵必须非负，这里使用伯努利模型。scikit-learn 朴素贝叶斯伯努利模型类及参数如下：

sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)

其中：

• alpha 表示平滑参数，如拉普拉斯平滑则 alpha=1。
• fit_prior 表示是否使用先验概率，默认为 True。
• class_prior 表示类的先验概率。

常用方法:

• fit(x,y)选择合适的贝叶斯分类器。
• predict(X) 对数据集进行预测返回预测结果。

from sklearn.naive_bayes import BernoulliNB

model = BernoulliNB()  # 定义伯努利模型分类器
model.fit(X_train, y_train)  # 模型训练
y_pred = model.predict(X_test)  # 模型预测
y_pred

当我们训练好模型并进行分类预测之后，可以通过比对预测结果和真实结果得到预测的准确率。

from sklearn.metrics import accuracy_score

accuracy_score(y_test, y_pred)

可以看到，通过朴素贝叶斯算法进行分类可以得到准确率为 95%，效果还是非常不错的。

小结

这篇文章从概率论的相关概念讲起，阐述了朴素贝叶斯算法的核心定理，即贝叶斯定理。同时，实验应用理论结合代码的方式讲解了朴素贝叶斯的原理以及实现过程。特别注意的是，朴素贝叶斯算法中涉及到的概率论知识点容易混淆，建议通过结合实际的示例进行区分。

系列文章

• 综述及示例
• 线性回归实现与应用
• 多项式回归实现与应用
• 岭回归和 LASSO 回归实现
• 回归模型评价与检验
• 逻辑回归实现与应用
• K-近邻算法实现与应用
• 朴素贝叶斯实现及应用
• 分类模型评价方法
• 支持向量机实现与应用
• 决策树实现与应用
• 装袋和提升集成学习方法
• 划分聚类方法实现与应用
• 层次聚类方法实现与应用
• 主成分分析原理及应用
• 密度聚类方法实现与应用
• 谱聚类及其他聚类方法应用
• 自动化机器学习综述
• 自动化机器学习实践应用
• 模型动态增量训练
• 模型推理与部署