机器学习：主成分分析原理及应用

6670 字 · 220 阅读 · 2023 年 05 月 15 日

介绍

在多元统计分析中，主成分分析（Principal components analysis，PCA）是一种分析、简化数据集的技术。经常用于减少数据集的维数，同时保留数据集中的对方差贡献最大的特征。PCA 也是十分常用的降维技术，其本质也可以看作是在最大化保留原始数据的情况下对数据做映射。这篇文章将会对该技术进行剖析，从基本的数学知识入手，逐渐深入该方法。

本篇文章需特别授权许可，内容版权归作者所有，未经授权，禁止转载。

知识点

向量的基
向量映射
方差和协方差
特征值和特征向量
主成分分析计算

向量的基

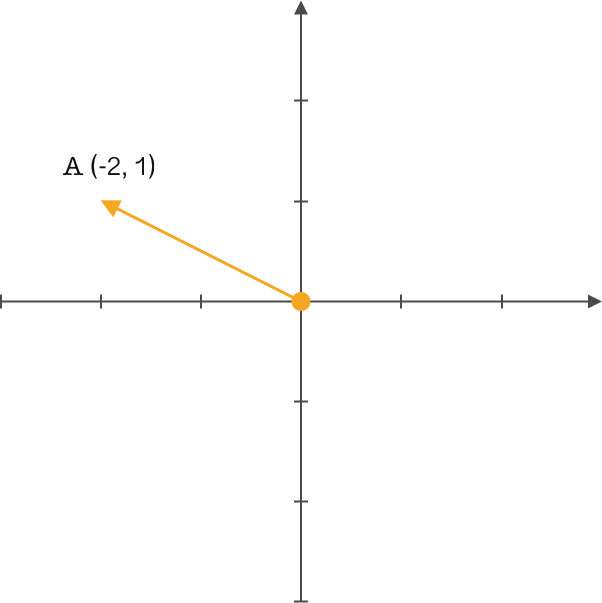
对于向量这个词想必你应该并不陌生，如下图所示，在一个二维笛卡尔直角坐标系中，你是如何定义向量 $A$ 的呢？

$A(-2,1)$ 这应该是大家想到的结果。没错，在高中时期我们通常都会这样定义。但线性代数中就会有另一个概念：基。

基（basis）也称为基底，其是用于描述、刻画向量空间的基本工具。向量空间的基是它的一个特殊的子集，基的元素称为基向量。向量空间中任意一个元素，都可以唯一地表示成基向量的线性组合，使用基底可以便利地描述向量空间。

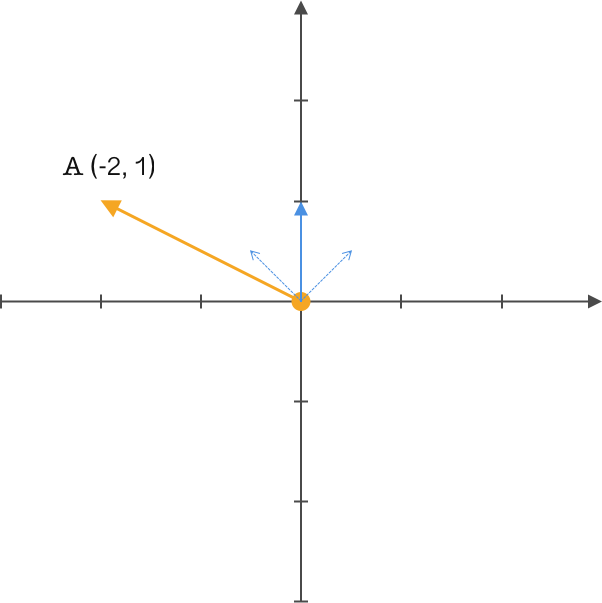
由此单凭向量的终点坐标是不能完整的表述一个向量，通过引入基向量则能够精确的表述该问题。通常我们的描述都是隐式的引入了一个定义：以 $x$、$y$ 轴的正方向且长度为 1 的 $(1,0)$ 和 $(0,1)$ 基向量作为标准。此时向量 $A$ 在 $x$ 上的投影为 2，$y$ 上的投影为 1，再通过基向量的方向确定表达式为 $(-2,1)$ 。

上面图片和描述中我们默认选择了 $(1,0)$ 、 $(0,1)$ 这对在 $x$、$y$ 轴上且长度为一的正交基向量，只是便于与二维坐标相对应，实际上任何两条线性无关的向量都可以作为一组基，因此我们得到一个结论：首先在空间中确定一组基，其次将向量在该基所在直线上的投影表示出来就是该向量的准确描述。

重新定义向量

目前，我们已知空间中任何一组基都可以重新定义或描述一个向量。接下来，我们就来举个例子。

同样我们使用上面的 $A$ 向量，但我们改变原来的基为 $(1,1)$ 和 $(-1,1)$ 。前面提到过，一般都喜欢将基的模长定义为 1，因为这样能简化运算，向量乘基直接就能得到新基上的坐标，所以我们标准化这组基的模长为 1，得到 $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 和 $(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 。很简单的转换，只需要对原来基的模做运算即可。

通过简单的变换现在我们得到了一组新基，并且模长为 $1$，接下来就可以通过这组基来重新定义向量 $A$ 了。如何转换 $A$ 向量呢？平移还是旋转，下面我们通过简单的矩阵运算角度来认识这个问题。

$$ \left( \begin{array}{cc}{\frac{\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}} \\ {-\frac{\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}}\end{array}\right) \left( \begin{array}{c}{-2} \\ {1}\end{array}\right)=\left( \begin{array}{c}{-\frac{\sqrt{2}}{2}} \\ {\frac{3 \sqrt{2}}{2}}\end{array}\right)$$

我们将基按照行排列成矩阵，将向量按照列排列成矩阵，做矩阵的乘法得到一个新矩阵，此时矩阵中的 $(-\frac{\sqrt{2}}{2},\frac{3\sqrt{2}}{2})$ 便是向量 $A$ $(-2,1)$ 在基 $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 和 $(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 上的新定义。

你应该会有这样的疑问，为什么基于向量做矩阵运算就能得到向量在新基上的重新定义？下面我们就来简单探讨一下这个问题。

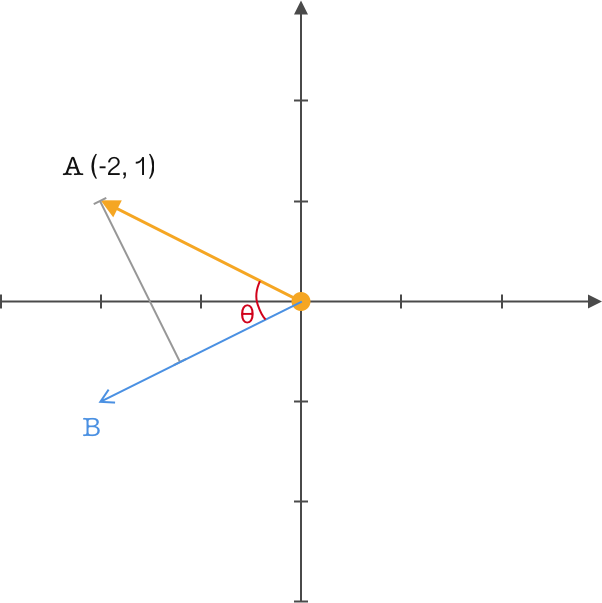
我们在向量 $A$ 的图中再定义了一个向量 $B$，并从向量 $A$ 做投影到向量 $B$ ，两个向量之间的夹角为 $θ$，同时对它们做内积运算，得到一个熟悉的公式：

$$ A\cdot B=\left | A \right |\left | B \right |cos(\theta )$$

关键的地方来了，前面我们一直强调将基的模长取值为 $1$，从而便于转换定义，这里我们就来实际运用一下。设置向量 $B$ 的模长为 $1$，那么上面的公式就可以变为：

$$ A\cdot B=\left | A \right |cos(\theta )$$

此时可以得到一个结论：两个向量相乘，且其中一个模长为 $1$，那么结果就是该向量在另一个向量上投影的矢量距离。

现在转换到上面的内容就一目了然了，向量 $B$ 模长为 $1$，与我们定义的新基一致，由于只有一个基，所以不存在线性关系，通过向量 $A$ 与该组基做矩阵运算最终便得到了新的映射。

重新定义矩阵

前面使用不同的基，实现了对向量的重新映射，同样通过一个简单的矩阵运算来说明了这个问题。下面我们接着引入一些新知识对矩阵也做定义。

我们通过一组新基重新映射了一个向量，若此时有多个向量又该如何映射？当然还是可以通过矩阵来轻松搞定，下面使用一组基来映射多个向量：

$$ \left( \begin{array}{cc}{\frac{\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}} \\ {-\frac{\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}}\end{array}\right) \left( \begin{array}{cccc}{-2} & {2} & {-2} & {2} \\ {1} & {1} & {-1} & {-1}\end{array}\right)=\left( \begin{array}{cccc}{\frac{-\sqrt{2}}{2}} & {\frac{3 \sqrt{2}}{2}} & {\frac{-3 \sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}} \\ {\frac{3 \sqrt{2}}{2}} & {\frac{-\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}} & {\frac{-3 \sqrt{2}}{2}}\end{array}\right)$$

在基不变的情况下，我们增加了三个按列排列的二维向量。可以看到，矩阵帮助我们快速的将原来按 $(1,0)$ 和 $(0,1)$ 定义的向量全部映射到 $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 和 $(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 上

这里简单的解释下上面三个矩阵的含义，第一个矩阵表示将两个基按行排列；第二个矩阵表示将四个向量按列排列；第三个矩阵表示将第二个矩阵作用到第一个矩阵所在基的新映射，此时每一列对应第二个矩阵的每一列。

除此之外，与之对应的改变基的数量，我们来看看结果如何：

$$ \left( \begin{array}{cc}{\frac{\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}} \\ {\frac{-\sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}} \\ {\frac{\sqrt{2}}{2}} & {\frac{-\sqrt{2}}{2}}\end{array}\right) \left( \begin{array}{cc}{-2} & {2} \\ {1} & {1}\end{array}\right)=\left( \begin{array}{cc}{\frac{-\sqrt{2}}{2}} & {\frac{3 \sqrt{2}}{2}} \\ {\frac{3 \sqrt{2}}{2}} & {\frac{-\sqrt{2}}{2}} \\ {\frac{-3 \sqrt{2}}{2}} & {\frac{\sqrt{2}}{2}}\end{array}\right)$$

可以发现在增加了一个基后，原来的二维向量映射成了一个三维向量。是不是有种恍然大悟的感觉，改变基的数量就可以改变向量的维数，那么同样如果减少基的数量为 $1$，向量就会减少维数。似乎这里与我们的主题降维就有了一点关联了。

下面将矩阵升高维度，使用 $i$ 个 $k$ 维的 $M$ 向量矩阵与 $j$ 个 $k$ 维的 $N$ 向量矩阵做运算，通过数学方式做下面定义：

$$ \left( \begin{array}{c}{M_{1}} \\ {M_{2}} \\ {\vdots} \\ {M_{i}}\end{array}\right) \left( \begin{array}{cccc}{N_{1}} & {N_{2}} & {\dots} & {N_{j}}\end{array}\right)=\left( \begin{array}{cccc}{M_{1} N_{1}} & {M_{1} N_{2}} & {\cdots} & {M_{1} N_{j}} \\ {M_{2} N_{1}} & {M_{2} N_{2}} & {\cdots} & {M_{2} N_{j}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {M_{i} N_{1}} & {M_{i} N_{2}} & {\cdots} & {M_{i} N_{j}}\end{array}\right)$$

结合上面我们的结论来分析该表达式，可以看出我们将 $j$ 个按列组成的向量映射到了 $i$ 个按行排列的基中得到一个 $i$ 行 $j$ 列的矩阵。此时减小 $i$ 的取值也就是减少了基的数量，矩阵运算便后得到相对低维映射的矩阵。这里通过高维函数表达式再次验证了基的数量决定了向量映射后的维数。

主成分分析 PCA

做了这么多的铺垫，终于到了这篇文章的核心问题。通过前面的叙述我们已经知道了基的个数决定着向量映射后的维数。所以问题得到了转换，现在需要做的就是找到最优并且数量合适的基。

还记得实验开头对主成分分析的描述吗？「保持数据集中的对方差贡献最大的特征」这是主成分分析使用的一个特点也是要求。在对方差理解前我们先从为什么需要引入方差开始说明。

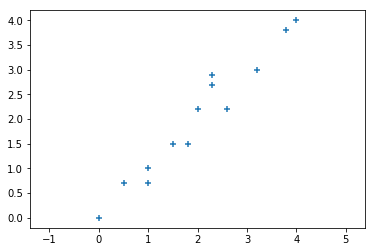
在二维空间中有如下图中的一些数据点：

可以看到数据点的 $x$ 与 $y$ 之间的相关性很强，所以数据就会出现冗余。我们可以对该数据进行降维处理，也就是降到一维，通过一个维度来表现该二维数据。

现在你应该能联想到若选择一个最优基与该二维数据做矩阵运算，便可实现降维。关于基的选择，其实比较直观想到的就是在一、三象限之间的对角线。为什么会有这个想法，因为使用该基来映射数据数据点后看起来和原来最数据点分布最相近，同时投影也使得数据点最分散，即投影后的数据的方差最大，这样降维的同时也最大化的保留原始数据的信息。

若使用 $x$ 或 $y$ 轴进行投影，可以清楚的观察到很多点在投影后会重合，相当于数据的丢失，这也是为什么投影要最分散的原因。

下面通过代码来演示降维的操作，首先加载上面的数据点：

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.array([0, 0.5, 1, 1, 1.5, 1.8, 2, 2.3, 2.3, 2.6, 3.2, 3.8, 4])
y = np.array([0, 0.7, 1, 0.7, 1.5, 1.5, 2.2, 2.9, 2.7, 2.2, 3, 3.8, 4])

arr = np.array([x, y])
plt.axis("equal")
plt.scatter(x, y, marker='+')

直观上我们选择一象限副对角线作为基，并且标准化模长为 $1$，最终为 $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ 。

base = np.array([np.sqrt(2)/2, np.sqrt(2)/2])  # 基向量
base

接着就是做两者的矩阵运算，得到降维后的数据。

result_eye = np.dot(base, arr)
result_eye

现在，我们得到了降维后的一维数组。由于一维数组无法在二维平面可视化，所以这里也无法与原数据进行可视化对比。

前面，我们通过肉眼观察数据非分布趋势来选择降维的基，效果还不错。但如果原始数据的维数很大超过二维空间，无法观察数据分布该如何选择基呢？所以，接下来还需要继续探讨。

方差和协方差

统计学中，方差是用来度量单个随机变量的离散程度。也就是说，最大方差给出了数据最重要的信息。如上面的例子，数据点投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述。一个维度中的方差，可以看作是该维度中每个元素与其均值的差平方和的均值，公式如下：

$$ var(x) = \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X})(X_{i}-\bar{X})$$

因此，我们的目标变成：

找到一个基，通过这个基映射原来的二维数据点，得到一个方差最大的结果，从而完成降维的目的。

上面二维降成一维时，我们寻找使得该数据集最大方差的一个基，容易联想到从更高维降到低维时，步骤应该是先寻找第一个最大方差的基，接着寻找第二个次大方差的基，依次找到相应维数的基的数量。

想法看似符合逻辑，但实际上是有问题的。单纯这样选择会使得后面一个基的方向与前面一个基的方向几乎重合，这样得到的维度是没有意义的。所以限制条件来了，在不断寻找最大方差基的同时，我们需要两个基之间是没有相关性的，也就是两者独立，这样获得的基之间是没有重复性的。

如何才能使得两个向量之间独立？在二维空间中两个向量垂直，则线性无关，那么在高维空间中，向量之间相互正交，则线性无关。

接着我们深入方差，方差其实是一种特殊的结构，可以看到上面的公式中两个变量相同都是 $(X_{i}-\bar{X})$ ，用来衡量两个相同变量的误差，那如果两个变量不同呢？我们变换变量 $(X_{i}-\bar{X})$ 为 $(Y_{i}-\bar{Y})$ ，那方差公式就变成了：

$$ cov(x) = \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X})(Y_{i}-\bar{Y})$$

可以得到：$cov(x,x) = var(x)$

实际上这个叫协方差，协方差一般用来刻画两个随机变量的相似程度。也就是从原来衡量两个相同变量的误差，到现在变成了衡量两个不同变量的误差。通俗点可以理解为：两个变量在变化过程中是否同向变化？还是反方向变化？同向或反向程度如何？

好巧，似乎协方差就能表述两个向量之间的相关性，按照前面选择基的要求时需要基之间相互正交，那么让两个变量之间的协方差等于 $0$ 不就可以了吗？因此，选择时让下一个基与上一个基之间的协方差等于 $0$，那么得到的两个基必然是相互正交的。

协方差矩阵

上一段内容我们通过方差到协方差已经了解并解决了如何选择正交基，从而达到降维的要求。可是从协方差的公式中又出现了新问题。协方差最多只能衡量两个变量之间的误差，如果有 $n$ 个向量则需要计算 $\frac{n!}{(n-2)!*2}$ 个协方差。因此我们继续扩展问题到多向量。通过协方差的定义来计算任意两个变量的关系：

$$ C(x_{a},x_{b})=\frac{1}{n}\sum_{i=1}^{n}(x_{ai}-\bar{x}_{a})(x_{bi}-\bar{x}_{b})$$

下面，我们以向量个数等于 $3$ 为例，我们转变为矩阵的表示形式：

$$ C \left( \begin{array}{ccc}{\operatorname{cov}(x, x)} & {\operatorname{cov}(x, y)} & {\operatorname{cov}(x, z)} \\ {\operatorname{cov}(y, x)} & {\operatorname{cov}(y, y)} & {\operatorname{cov}(y, z)} \\ {\operatorname{cov}(z, x)} & {\operatorname{cov}(z, y)} & {\operatorname{cov}(z, z)}\end{array}\right)$$

从矩阵中会发现协方差矩阵其实就是由对角线的方差与非对角线的协方差构成，所以协方差矩阵的核心理解：由向量自身的方差与向量之间的协方差构成。这个定义延伸到更多向量时同样受用。

所以协方差矩阵就是解决 PCA 问题的关键，终于问题又有了突破口。通过前面的讲解，现在问题可以简化为：

选择一组基，使得原始向量通过该基映射到新的维度，同时需要满足使得该向量的方差最大，向量之间的协方差为 $0$ ，也就是矩阵对角化。

特征值和特征向量

目前问题已经很浅显易懂了，首先得到向量数据的协方差矩阵，其次通过协方差矩阵对方差与协方差的处理获得用于降维的基。找到问题后，接下来就是如何解决问题了。

再观察一下协方差矩阵，我们可以发现其实它是一个对称矩阵。在矩阵中对称矩阵有很多特殊的性质，例如，如果对其进行特征分解，那么就会得到两个概念：↗ 特征值与特征向量。由于是对称矩阵，所以特征值所对应的特征向量一定无线性关系，即相互之间一定正交，内积为零。

在线性代数中给定一个方阵 $A$ ，它的特征向量 $v$ 在 $A$ 变换的作用下，得到的新向量仍然与原来的 $v$ 保持在同一条直线上，且仅仅在尺度上变为原来的 $\lambda$ 倍。则称 $v$ 是 $A$ 的一个特征向量，$\lambda$ 是对应的特征值，即：

$$ Av = \lambda v$$

这里的特征向量 $v$ 也就是矩阵 $A$ 的主成分，而 $\lambda$ 则是其对应的权值也就是各主成分的方差大小。

至此，我们的目的就是寻找主成分，所以问题就转变成了寻找包含主成分最多的特征向量 $v$，但是这个 $v$ 并不好直观的度量，由此我们可以转变为寻找与之对应的权值 $\lambda$，$\lambda$ 越大则所对应的特征向量包含的主成分也就越多，所以问题接着转变为了寻找最大值的特征值 $\lambda$。

所以，问题基本上已经得到了解决：

通过计算向量矩阵得到其协方差矩阵，然后特征分解协方差矩阵得到包含主成分的特征向量与对应的特征值，最后通过特征值的大小排序后依次筛选出需要用于降维的特征向量个数。

在前面小节中我们选择了肉眼观察的一组基对二位数据进行降维，下面我们尝试利用协方差矩阵的思想来对同样的数据做降维处理。

首先求得协方差矩阵，通过 NumPy 的 $cov$ 函数来实现

covMat = np.cov(arr)  # 计算协方差矩阵
covMat

接下来利用 NumPy 中的线性代数工具 linalg 特征分解协方差矩阵得到特征值、特征向量

eigVal, eigVec = np.linalg.eig(np.mat(covMat))  # 获得特征值、特征向量
eigVal, eigVec

然后，我们根据特征值来选择特征向量。对特征值降序排序，取第一个特征向量。

eigValInd = np.argsort(-eigVal)  # 特征值降序排序
bestVec = eigVec[:, eigValInd[:1]]  # 取最好的一个特征向量
bestVec

最后，利用该特征向量对前面的示例数据降维，得到一维数据：

result_cov = np.dot(arr.T, bestVec)
result_cov

现在，我们来绘制出通过最优特征向量和前面肉眼观察的一组基各自降维的结果。

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].scatter(result_cov.flatten().A[0], [
                0 for i in range(len(x))], marker='+')
axes[1].scatter(result_eye, [0 for i in range(len(x))], marker='+')

由于上面是一维数组的二维展示，我们看不出太多的信息。所以，下面通过度量两者的方差，比较谁更好：

np.var(result_cov), np.var(result_eye)

可以看到，通过分解协方差矩阵来降维得到结果的方差要大一点，这也就代表了保留的原始数据信息更多。看来，眼睛的确不如数学方法可靠。

高维数据降维处理

前面的例子中，为了便于教学只分析了二维数据降到一维的过程。下面，我们将对一个包含 590 个特征的数据集进行降维处理。

$590$ 个特征不算太多，但也是一个很大的维度了。所以，这里使用降维的方式处理数据集，得到一个维度更低，但仍然保留绝大部分的原始信息的新数据集。

首先，通过下面的链接加载数据并预览数据集。

import pandas as pd

df = pd.read_csv("http://labfile.oss.aliyuncs.com/courses/1211/pca_data.csv")
df.describe()

可以看到，数据集拥有 1567 个样本，每个样本拥有 590 个特征。

在进行得到协方差矩阵处理前，我们会对数据按维度进行零均值化处理。其主要目的是去除均值对变换的影响，减去均值后数据的信息量没有变化，即数据的区分度（方差）是不变的。如果不去均值，第一主成分，可能会或多或少的与均值相关。前面的例子我们省略了这一步，是为了能更好的观察绘制出来的图像，且当时并无太大影响。

data = df.values
mean = np.mean(data, axis=0)
data = data - mean
data

接下来，计算协方差矩阵：

covMat = np.cov(data, rowvar=False)
covMat

然后，分解协方差矩阵获得特征值与特征向量，同时绘制出前 30 个特征值变化曲线图。

eigVal, eigVec = np.linalg.eig(np.mat(covMat))
plt.plot(eigVal[:30], marker='o')

可以看到方差的急剧下降，到后面绝大多数的主成分所占方差几乎为 $0$，因此更说明了对该数据进行主成分分析的必要性。其中，第 4 个点是比较明显的拐点。

这里，我们计算前 4 个主成分所占的方差数值与 90% 主成分的方差总和数值：

sum(eigVal[:4]), sum(eigVal)*0.9

观察两者的数值大小，可以发现在 590 个主成分中，前 4 个主成分所占的方差就已经超过了 90%。说明后 586 个主成分仅占 10% ，即仅用前 4 个特征向量来映射数据，就可以保留绝大多数的原始数据信息。

接下来，我们取得最好的 4 个特征向量，并计算最终的降维数据。

eigValInd = np.argsort(-eigVal)  # 特征值降序排序
bestVec = eigVec[:, eigValInd[:4]]  # 取最好的 4 个特征向量
bestVec

np.dot(data, bestVec)

前面的文章中，我们已经学习了 scikit-learn 主成分分析方法 sklearn.decomposition.PCA，下面我们通过该方法来计算示例数据降维后的结果。

from sklearn.decomposition import PCA

pca = PCA(n_components=4)
pca.fit_transform(data)

通过观察 sklearn.decomposition.PCA 的源码，我们可以发现它在对矩阵进行分解时使用的是 linalg.svd 方法。该方法可以直接对原始矩阵进行矩阵分解，并且能对非方阵矩阵分解，而我们在推导时使用的是 linalg.eig 方法。向量为矢量，两者分解后的参考不同，所以获得特征向量的符号存在差异，进而导致根据特征向量映射的降维矩阵也存在符号的差异，但这并不会影响降维结果。

由此可以看到，scikit-learn 提供的方法处理结果与我们自己分析得到的结果基本一致，不过一般情况下都直接使用 sklearn.decomposition.PCA 即可，该 API 在诸多方面都进行了优化，也包含更多的可选参数。

小结

这篇文章中，我们通过从向量入手介绍了基，接着用矩阵来进行推导降维，并且引入了主成分分析最重要的概念方差、协方差、协方差矩阵，最后通过利用特征值与特征向量来达到降维。由浅入深的了解了主成分分析的相关知识点，想必现在你应该对主成分分析已经有了一个完整且熟练的掌握。

系列文章

本篇文章需特别授权许可，内容版权归作者所有，未经授权，禁止转载。

BY-ND 4.0

Comments

△