K-近邻算法实现与应用
介绍
在解决分类问题的过程中,K-近邻算法(简称:KNN)是一种简单而且实用的方法。这篇文章将对 K-近邻算法进行详细的介绍,并从距离计算,分类决策等方面熟悉 K-近邻算法的原理及 Python 实现,最后,运用 K-近邻算法构建预测模型,并实现对丁香花分类。
知识点
- 最近邻算法
- K-近邻算法
- 决策规则
- KNN 算法实现
最近邻算法
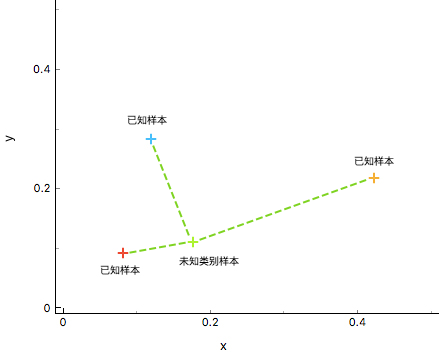
介绍 K-近邻算法之前,首先说一说最近邻算法。最近邻算法(Nearest Neighbor,简称:NN),其针对未知类别数据 $x$,在训练集中找到与 $x$ 最相似的训练样本 $y$,用 $y$ 的样本对应的类别作为未知类别数据 $x$ 的类别,从而达到分类的效果。
如上图所示,通过计算数据 $X_{u}$ (未知样本)和已知类别 ${\omega_{1},\omega_{2},\omega_{3}}$ (已知样本)之间的距离,判断 $X_{u}$ 与不同训练集的相似度,最终判断 $X_{u}$ 的类别。显然,这里将 绿色未知样本 类别判定与 红色已知样本 类别相同较为合适。
K-近邻算法
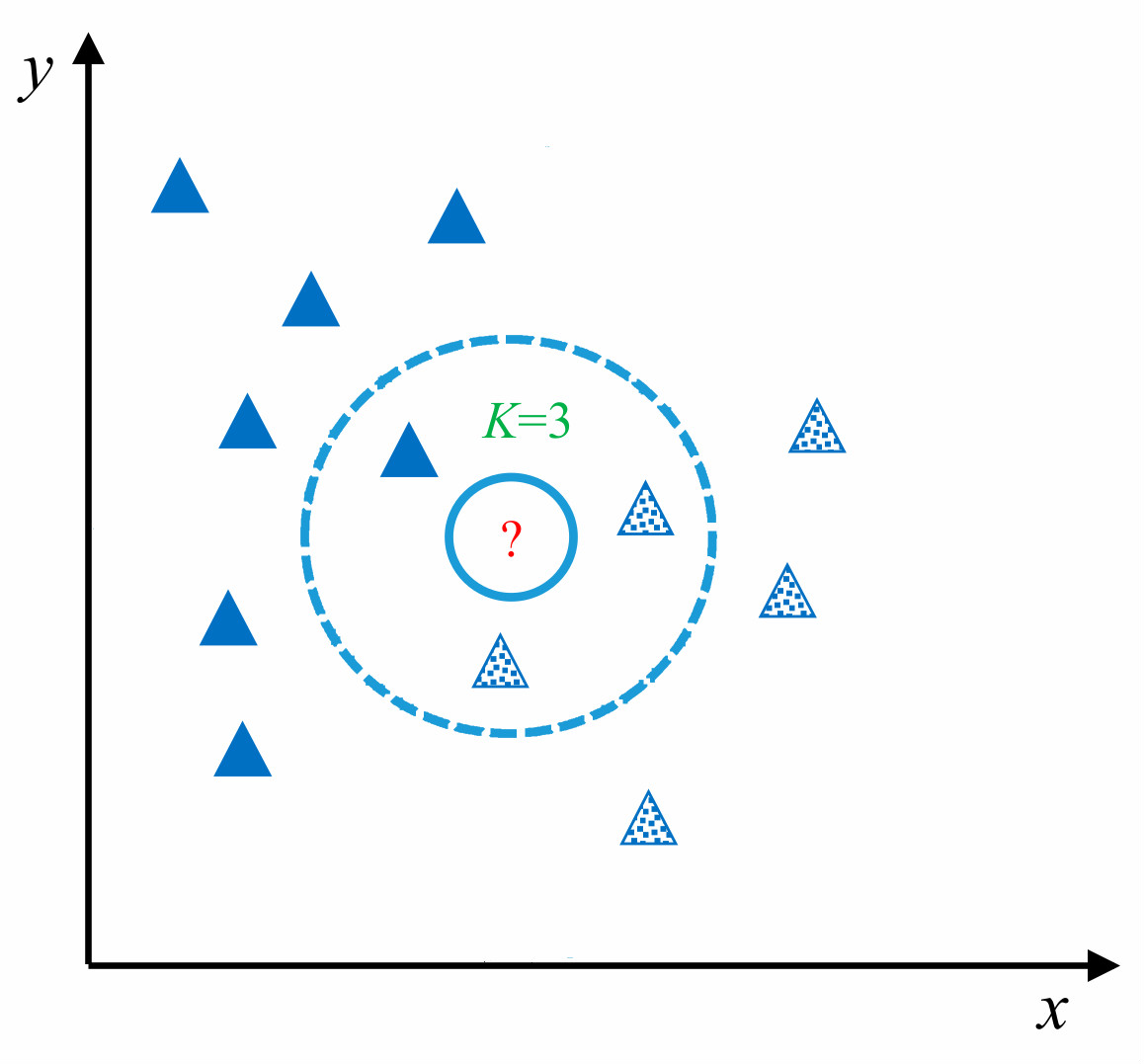
K-近邻(K-Nearest Neighbors,简称:KNN)算法是最近邻(NN)算法的一个推广,也是机器学习分类算法中最简单的方法之一。KNN 算法的核心思想和最近邻算法思想相似,都是通过寻找和未知样本相似的类别进行分类。但 NN 算法中只依赖 1 个样本进行决策,在分类时过于绝对,会造成分类效果差的情况,为解决 NN 算法的缺陷,KNN 算法采用 K 个相邻样本的方式共同决策未知样本的类别,这样在决策中容错率相对于 NN 算法就要高很多,分类效果也会更好。
如上图所示,对于未知测试样本(图中 ?所示)采用 KNN 算法进行分类,首先计算未知样本和训练样本之间的相似度,找出最近 K 个相邻样本(在图中 K 值为 3,圈定距离 ?最近的 3 个样本),再根据最近的 K 个样本最终判断未知样本的类别。
K-近邻算法实现
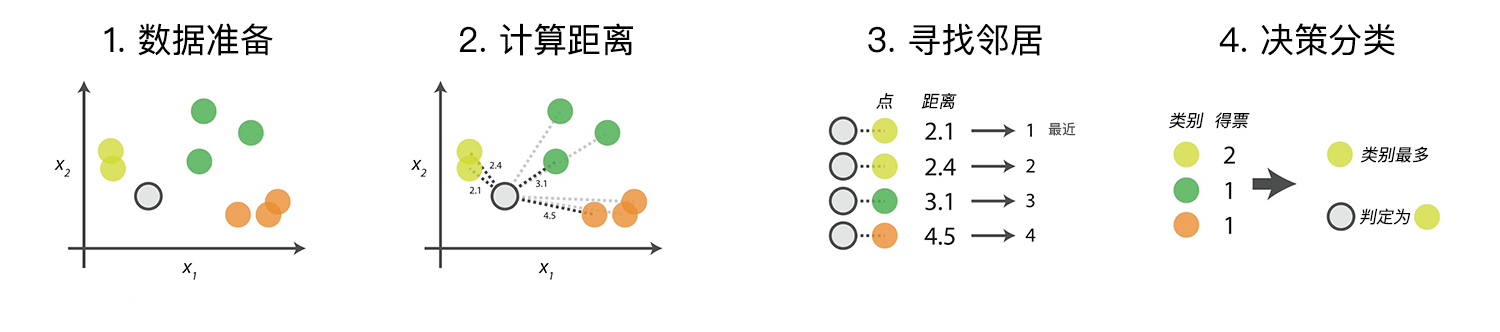
KNN 算法在理论上已经非常成熟,其简单、易于理解的思想以及良好的分类准确度使得 KNN 算法应用非常广泛。算法的具体流程主要是以下的 4 个步骤:
- 数据准备:通过数据清洗,数据处理,将每条数据整理成向量。
- 计算距离:计算测试数据与训练数据之间的距离。
- 寻找邻居:找到与测试数据距离最近的 K 个训练数据样本。
- 决策分类:根据决策规则,从 K 个邻居得到测试数据的类别。
下面,我们尝试完成一个 KNN 分类流程。首先,生成一组示例数据,共包含 2 个类别 $A$ 和 $B$,其中每一条数据包含两个特征 $x$ 和 $y$。
import numpy as np
def create_data():
features = np.array(
[[2.88, 3.05], [3.1, 2.45], [3.05, 2.8], [2.9, 2.7], [2.75, 3.4],
[3.23, 2.9], [3.2, 3.75], [3.5, 2.9], [3.65, 3.6], [3.35, 3.3]])
labels = ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B']
return features, labels
然后,我们尝试加载并打印这些数据。
features, labels = create_data()
print('features: \n', features)
print('labels: \n', labels)
为了更直观地理解数据,接下来用 Matplotlib 下的 pyplot 包来对数据集进行可视化。为了代码的简洁,我们使用了 map 函数和 lambda 表达式对数据进行处理。如果你对这两个方法不太了解,需要自学相应的 Python 知识。
from matplotlib import pyplot as plt
%matplotlib inline
plt.figure(figsize=(5, 5))
plt.xlim((2.4, 3.8))
plt.ylim((2.4, 3.8))
x_feature = list(map(lambda x: x[0], features)) # 返回每个数据的x特征值
y_feature = list(map(lambda y: y[1], features))
plt.scatter(x_feature[:5], y_feature[:5], c="b") # 在画布上绘画出"A"类标签的数据点
plt.scatter(x_feature[5:], y_feature[5:], c="g")
plt.scatter([3.18], [3.15], c="r", marker="x") # 待测试点的坐标为 [3.1,3.2]
由上图所示,标签为 $A$(蓝色圆点)的数据在画布的左下角位置,而标签为 $B$(绿色圆点)的数据在画布的右上角位置,通过图像可以清楚看出不同标签数据的分布情况。其中 红色 x 点 即表示这篇文章需预测类别的测试数据。
距离度量
在计算两个样本间的相似度时,可以通过计算样本之间特征值的距离进行表示。若两个样本距离值越大(相距越远),则表示两个样本相似度低,相反,若两个样本值越小(相距越近),则表示两个样本相似度越高。
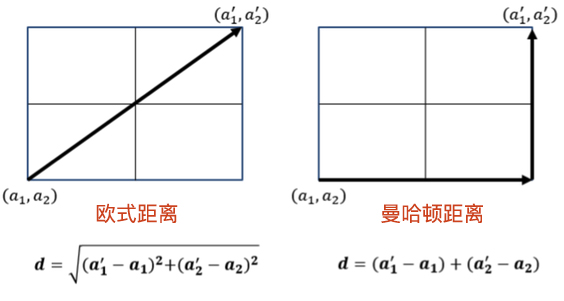
计算距离的方法有很多,这篇文章介绍两个最为常用的距离公式:曼哈顿距离 和 欧式距离。这两个距离的计算图示如下:
曼哈顿距离
曼哈顿距离又称马氏距离,是计算距离最简单的方式之一。公式如下:
其中:
- $X$, $Y$:两个数据点
- $N$:每个数据中有 $N$ 个特征值
- $X_{i}$ :数据 $X$ 的第 $i$ 个特征值
公式表示为将两个数据 $X$ 和 $Y$ 中每一个对应特征值之间差值的绝对值,再求和,便得到曼哈顿距离。
def d_man(x, y):
d = np.sum(np.abs(x - y))
return d
x = np.array([3.1, 3.2]) # 任意指定 2 点计算
print("x:", x)
y = np.array([2.5, 2.8])
print("y:", y)
print(d_man(x, y))
欧式距离
欧式距离源自 $N$ 维欧氏空间中两点之间的距离公式。表达式如下:
其中:
- $X$, $Y$ :两个数据点
- $N$:每个数据中有 $N$ 个特征值
- $X_{i}$ :数据 $X$ 的第 $i$ 个特征值
公式表示为将两个数据 $X$ 和 $Y$ 中的每一个对应特征值之间差值的平方,再求和,最后开平方,便是欧式距离。
def d_euc(x, y):
d = np.sqrt(np.sum(np.square(x - y)))
return d
x = np.random.random(10) # 随机生成 10 个数的数组作为 x 特征的值
print("x:", x)
y = np.random.random(10)
print("y:", y)
distance_euc = d_euc(x, y)
print(distance_euc)
决策规则
在得到测试样本和训练样本之间的相似度后,通过相似度的排名,可以得到每一个测试样本的 K 个相邻的训练样本,那如何通过 K 个邻居来判断测试样本的最终类别呢?可以根据数据特征对决策规则进行选取,不同的决策规则会产生不同的预测结果,最常用的决策规则是:
- 多数表决法:多数表决法类似于投票的过程,也就是在 K 个邻居中选择类别最多的种类作为测试样本的类别。
- 加权表决法:根据距离的远近,对近邻的投票进行加权,距离越近则权重越大,通过权重计算结果最大值的类为测试样本的类别。
我们这里推荐使用多数表决法,这种方法更加简单, 这篇文章前面的配图 即为多数表决法。
import operator
def majority_voting(class_count):
# 多数表决函数
sorted_class_count = sorted(
class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count
arr = {'A': 3, 'B': 2, "C": 6, "D": 5}
majority_voting(arr)
在多数表决法的定义中,我们导入了 operater 计算模块,目的是对字典类型结构排序。可以从结果中看出函数返回的结果为票数最多的 C,得票为 6 次。
KNN 算法实现
在学习完以上的各个步骤之后,KNN 算法也逐渐被勾勒出来。以下就是对 KNN 算法的完整实现,这篇文章的距离计算采用欧式距离,分类的决策规则为多数表决法,定义函数 knn_classify(),其中函数的参数包括:
test_data:用于分类的输入向量。train_data:输入的训练样本集。labels:样本数据的类标签向量。k:用于选择最近邻居的数目。
def knn_classify(test_data, train_data, labels, k):
# KNN 方法完整实现
distances = np.array([]) # 创建一个空的数组用于存放距离
for each_data in train_data: # 使用欧式距离计算数据相似度
d = d_euc(test_data, each_data)
distances = np.append(distances, d)
sorted_distance_index = distances.argsort() # 获取按距离从小到大排序后的索引
sorted_distance = np.sort(distances)
r = (sorted_distance[k]+sorted_distance[k-1])/2 # 计算
class_count = {}
for i in range(k): # 多数表决
vote_label = labels[sorted_distance_index[i]]
class_count[vote_label] = class_count.get(vote_label, 0) + 1
final_label = majority_voting(class_count)
return final_label, r
分类预测
在实现 KNN 算法之后,接下来就可以对我们未知数据 [3.18, 3.15] 开始分类,假定我们 K 值初始设定为 5,让我们看看分类的效果。
test_data = np.array([3.18, 3.15])
final_label, r = knn_classify(test_data, features, labels, 5)
final_label
可视化展示
在对数据 [3.18, 3.15] 实现分类之后,接下来我们同样用画图的方式形象化展示 KNN 算法决策方式。
def circle(r, a, b): # 为了画出圆,这里采用极坐标的方式对圆进行表示 :x=r*cosθ,y=r*sinθ。
theta = np.arange(0, 2*np.pi, 0.01)
x = a+r * np.cos(theta)
y = b+r * np.sin(theta)
return x, y
k_circle_x, k_circle_y = circle(r, 3.18, 3.15)
plt.figure(figsize=(5, 5))
plt.xlim((2.4, 3.8))
plt.ylim((2.4, 3.8))
x_feature = list(map(lambda x: x[0], features)) # 返回每个数据的 x 特征值
y_feature = list(map(lambda y: y[1], features))
plt.scatter(x_feature[:5], y_feature[:5], c="b") # 在画布上绘画出"A"类标签的数据点
plt.scatter(x_feature[5:], y_feature[5:], c="g")
plt.scatter([3.18], [3.15], c="r", marker="x") # 待测试点的坐标为 [3.1,3.2]
plt.plot(k_circle_x, k_circle_y)
如图所示,当我们 K 值为 5 时,与测试样本距离最近的 5 个训练数据(如蓝色圆圈所示)中属于 $B$ 类的有 3 个,属于 $A$ 类的有 2 个,根据多数表决法决策出测试样本的数据为 $B$ 类。
在 KNN 算法中,K 值的选择对数据的最终决策有很大的影响,下面我们引入 ipywidgets 模块更加清晰的反映 K 的选择对预测结果影响。其中 ipywidgets 模块是 jupyter 中的一个交互式模块,可以通过下拉菜单选择不同的 K 值进行判断并预测未知点最后的种类。
from ipywidgets import interact, fixed
def change_k(test_data, features, k):
final_label, r = knn_classify(test_data, features, labels, k)
k_circle_x, k_circle_y = circle(r, 3.18, 3.15)
plt.figure(figsize=(5, 5))
plt.xlim((2.4, 3.8))
plt.ylim((2.4, 3.8))
x_feature = list(map(lambda x: x[0], features)) # 返回每个数据的 x 特征值
y_feature = list(map(lambda y: y[1], features))
plt.scatter(x_feature[:5], y_feature[:5], c="b") # 在画布上绘画出"A"类标签的数据点
plt.scatter(x_feature[5:], y_feature[5:], c="g")
plt.scatter([3.18], [3.15], c="r", marker="x") # 待测试点的坐标为 [3.1,3.2]
plt.plot(k_circle_x, k_circle_y)
interact(change_k, test_data=fixed(test_data),
features=fixed(features), k=[3, 5, 7, 9]) # 可交互式绘图
从图中可以直观的看到,不同的 K 值预测出不同的结果。接下来,我们使用 KNN 算法对真实数据集进行分类预测。
加载数据集
本次使用的数据集为丁香花数据集course-9-syringa.csv,丁香花数据集包含 daphne,syringa 和 willow 等 3 个种类,其中每个种类包含 150 条数据,每条数据包含 4 个特征值:花萼长度,花萼宽度,花瓣长度,花瓣宽度。利用 Pandas 将其导入成 DataFrame 格式。
import pandas as pd
lilac_data = pd.read_csv(
'https://labfile.oss.aliyuncs.com/courses/1081/course-9-syringa.csv')
lilac_data.head() # 预览前 5 行
为了使我们对数据更加了解,同样我们用 plt 将各个数据的特征绘制出来。由于丁香花数据集有 4 个特征值,在二维空间中无法直接表示,所以只有采用特征组合的方式绘画特征分布图。下面将 4 个特征,进行两两组合得到 6 种情况,并采用子图的方式进行绘制。
"""绘制丁香花特征子图
"""
fig, axes = plt.subplots(2, 3, figsize=(20, 10)) # 构建生成 2*3 的画布,2 行 3 列
fig.subplots_adjust(hspace=0.3, wspace=0.2) # 定义每个画布内的行间隔和高间隔
axes[0, 0].set_xlabel("sepal_length") # 定义 x 轴坐标值
axes[0, 0].set_ylabel("sepal_width") # 定义 y 轴坐标值
axes[0, 0].scatter(lilac_data.sepal_length[:50],
lilac_data.sepal_width[:50], c="b")
axes[0, 0].scatter(lilac_data.sepal_length[50:100],
lilac_data.sepal_width[50:100], c="g")
axes[0, 0].scatter(lilac_data.sepal_length[100:],
lilac_data.sepal_width[100:], c="r")
axes[0, 0].legend(["daphne", "syringa", "willow"], loc=2) # 定义示例
axes[0, 1].set_xlabel("petal_length")
axes[0, 1].set_ylabel("petal_width")
axes[0, 1].scatter(lilac_data.petal_length[:50],
lilac_data.petal_width[:50], c="b")
axes[0, 1].scatter(lilac_data.petal_length[50:100],
lilac_data.petal_width[50:100], c="g")
axes[0, 1].scatter(lilac_data.petal_length[100:],
lilac_data.petal_width[100:], c="r")
axes[0, 2].set_xlabel("sepal_length")
axes[0, 2].set_ylabel("petal_length")
axes[0, 2].scatter(lilac_data.sepal_length[:50],
lilac_data.petal_length[:50], c="b")
axes[0, 2].scatter(lilac_data.sepal_length[50:100],
lilac_data.petal_length[50:100], c="g")
axes[0, 2].scatter(lilac_data.sepal_length[100:],
lilac_data.petal_length[100:], c="r")
axes[1, 0].set_xlabel("sepal_width")
axes[1, 0].set_ylabel("petal_width")
axes[1, 0].scatter(lilac_data.sepal_width[:50],
lilac_data.petal_width[:50], c="b")
axes[1, 0].scatter(lilac_data.sepal_width[50:100],
lilac_data.petal_width[50:100], c="g")
axes[1, 0].scatter(lilac_data.sepal_width[100:],
lilac_data.petal_width[100:], c="r")
axes[1, 1].set_xlabel("sepal_length")
axes[1, 1].set_ylabel("petal_width")
axes[1, 1].scatter(lilac_data.sepal_length[:50],
lilac_data.petal_width[:50], c="b")
axes[1, 1].scatter(lilac_data.sepal_length[50:100],
lilac_data.petal_width[50:100], c="g")
axes[1, 1].scatter(lilac_data.sepal_length[100:],
lilac_data.petal_width[100:], c="r")
axes[1, 2].set_xlabel("sepal_width")
axes[1, 2].set_ylabel("petal_length")
axes[1, 2].scatter(lilac_data.sepal_width[:50],
lilac_data.petal_length[:50], c="b")
axes[1, 2].scatter(lilac_data.sepal_width[50:100],
lilac_data.petal_length[50:100], c="g")
axes[1, 2].scatter(lilac_data.sepal_width[100:],
lilac_data.petal_length[100:], c="r")
由于该数据集与特征较多,所以通过特征组合的方式进行数据分布的展示。当遇到更多特征时,还可以通过数据特征降低维度的方式来进行数据分析,相应的方法会在后续内容中讲解。
训练测试数据划分
当得到一个数据集时,希望通过该数据集得到一个训练模型,我们常常将数据切分为两部分,一部分为训练集,一部分为测试集。根据经验,较好的切分方法为随机切分,切分比例为:70% 作为训练集,30% 作为测试集。
在此我们使用了 scikit-learn 模块的 train_test_split 函数完成数据集切分。
from sklearn.model_selection import train_test_split X_train,X_test, y_train, y_test =train_test_split(train_data,train_target,test_size=0.4, random_state=0)
其中:
X_train,X_test,y_train,y_test分别表示,切分后的特征的训练集,特征的测试集,标签的训练集,标签的测试集;其中特征和标签的值是一一对应的。train_data,train_target分别表示为待划分的特征集和待划分的标签集。test_size:测试样本所占比例。random_state:随机数种子,在需要重复实验时,保证在随机数种子一样时能得到一组一样的随机数。
from sklearn.model_selection import train_test_split
# 得到 lilac 数据集中 feature 的全部序列: sepal_length,sepal_width,petal_length,petal_width
feature_data = lilac_data.iloc[:, :-1]
label_data = lilac_data["labels"] # 得到 lilac 数据集中 label 的序列
X_train, X_test, y_train, y_test = train_test_split(
feature_data, label_data, test_size=0.3, random_state=2)
X_test # 输出 lilac_test 查看
训练模型
在之前实验部分我们已经通过 Python 按照流程实现 KNN 算法,在实战中,我们更常使用 scikit-learn 库中 KNN 函数实现数据的分类。
sklearn.neighbors.KNeighborsClassifier((n_neighbors=5, weights='uniform', algorithm='auto')
其中:
n_neighbors:k值,表示邻近个数,默认为5。weights: 决策规则选择,多数表决或加权表决,可用参数('uniform','distance')algorithm: 搜索算法选择(auto,kd_tree,ball_tree),包括逐一搜索,kd树搜索或ball树搜索
from sklearn.neighbors import KNeighborsClassifier
def sklearn_classify(train_data, label_data, test_data, k_num):
# 使用 sklearn 构建 KNN 预测模型
knn = KNeighborsClassifier(n_neighbors=k_num)
# 训练数据集
knn.fit(train_data, label_data)
# 预测
predict_label = knn.predict(test_data)
# 返回预测值
return predict_label
模型预测
在上面定义函数之后,接下来就是对丁香花数据集中分出的测试集进行分类,传入 X_train,y_train,X_test 以及 K 值 3,通过 KNN 算法分类后,输出测试集的分类结果。
# 使用测试数据进行预测
y_predict = sklearn_classify(X_train, y_train, X_test, 3)
y_predict
准确率计算
得到预测结果后,我们需要评估模型的表现,也就是得出模型预测的准确度。计算准确率就是比较预测值和真实值的差异,得到预测正确的样本数,将其除以测试集的总个数。
def get_accuracy(test_labels, pred_labels):
# 准确率计算函数
correct = np.sum(test_labels == pred_labels) # 计算预测正确的数据个数
n = len(test_labels) # 总测试集数据个数
accur = correct/n
return accur
通过以上准确率计算函数,按照以下代码可以得到测试数据的分类准确率。
get_accuracy(y_test, y_predict)
K 值选择
当 K 值选取为 3 时,可以看到准确率不高,分类效果不太理想。 K 值的选取一直都是一个热门的话题,至今也没有得到很好的解决方法,根据经验,K 值的选择最好不超过样本数量的平方根。所以可以通过遍历的方式选择合适的 K 值。以下我们从 2 到 10 中画出每一个 K 值的准确率从而获得最佳 K 值。
normal_accuracy = [] # 建立一个空的准确率列表
k_value = range(2, 11)
for k in k_value:
y_predict = sklearn_classify(X_train, y_train, X_test, k)
accuracy = get_accuracy(y_test, y_predict)
normal_accuracy.append(accuracy)
plt.xlabel("k")
plt.ylabel("accuracy")
new_ticks = np.linspace(0.6, 0.9, 10) # 设定 y 轴显示,从 0.6 到 0.9
plt.yticks(new_ticks)
plt.plot(k_value, normal_accuracy, c='r')
plt.grid(True) # 给画布增加网格
从图像中可以得到,当 K=4 和 K=6 时,模型准确率相当。但机器学习选择最优模型时,我们一般会考虑到模型的泛化能力,所以这里选择 K=4,也就是更简单的模型。
Kd 树
KNN 算法的易于理解,很大程度上由于在对 KNN 实现输入示例分类时所用方法是线性扫描,即输入示例与每一个训练示例做距离计算。正因如此,当数据量特别大时,这样的计算会非常耗时。为了提高 KNN 搜索效率,减少计算距离的次数,可以通过构建 Kd 树的方法提高计算效率。
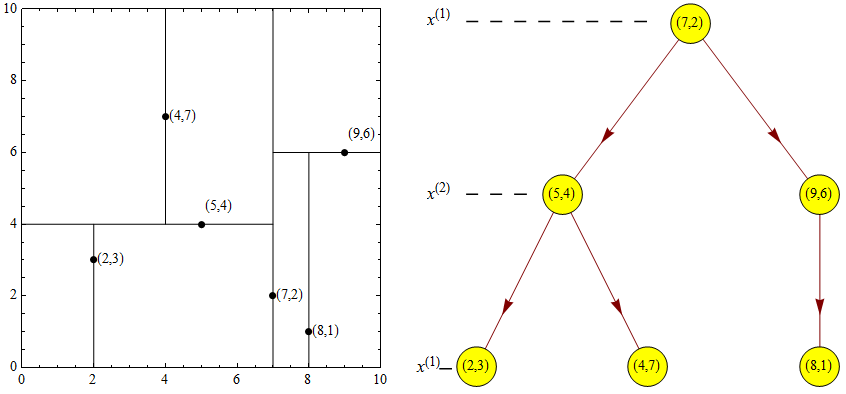
Kd 树(英文:K-dimension tree)是一种对 K 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。Kd 树是一种二叉树,表示对 K 维空间的一个划分,构造 Kd 树相当于不断地用垂直于坐标轴的超平面将 K 维空间切分,构成一系列的 K 维超矩形区域。Kd 树的每个结点对应于一个 K 维超矩形区域。利用 Kd 树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
Kd 树最邻近搜索
以下便是 Kd 树的最邻近搜索步骤:
- 从根节点开始,递归的往下移。往左还是往右的决定方法与插入元素的方法一样(如果输入点在分区面的左边则进入左子节点,在右边则进入右子节点)。
- 一旦移动到叶节点,将该节点当作「目前最佳点」。
-
解开递归,并对每个经过的节点运行下列步骤:
- 如果目前所在点比目前最佳点更靠近输入点,则将其变为目前最佳点。
- 检查另一边子树有没有更近的点,如果有则从该节点往下找
- 当根节点搜索完毕后完成最邻近搜索
通过步骤可以十分直观的发现,相比于传统 KNN 搜索遍历要节约很多时间和空间。
Kd 树实现
前面的讲解中,Kd 树的主要目的便是提高数据搜索的速度,减少内存和时间的消耗,以下我们就用代码来直观感受下 Kd 树的优点。采用 scikit-learn 库实现 Kd 树很简单,只需要在函数调用时传入 kd_tree 参数即可。
实际上 scikit-learn 提供的方法已不再是普通的 KNN 实现,而是集成了多种优化搜索方法,所以这里无法对比采用和未采用 Kd 树搜索的时间。默认的 algorithm='auto' 参数会自动选择优化搜索方法以减少训练用时。
kd_x = np.random.random((100000, 2)) # 生成 10 万条测试数据
kd_y = np.random.randint(4, size=(100000))
kd_knn = KNeighborsClassifier(n_neighbors=5, algorithm='kd_tree') # kd 树搜索
%time kd_knn.fit(kd_x, kd_y) # 输出 kd 树搜索训练用时
小结
这篇文章中学习了 KNN 算法的原理及 Python 实现,以及采用 scikit-learn 库对 KNN 算法的实现,KNN 算法虽然原理逻辑简单,但是在很多分类或者回归的例子中表现的非常好。
相关链接
系列文章
- 综述及示例
- 线性回归实现与应用
- 多项式回归实现与应用
- 岭回归和 LASSO 回归实现
- 回归模型评价与检验
- 逻辑回归实现与应用
- K-近邻算法实现与应用
- 朴素贝叶斯实现及应用
- 分类模型评价方法
- 支持向量机实现与应用
- 决策树实现与应用
- 装袋和提升集成学习方法
- 划分聚类方法实现与应用
- 层次聚类方法实现与应用
- 主成分分析原理及应用
- 密度聚类方法实现与应用
- 谱聚类及其他聚类方法应用
- 自动化机器学习综述
- 自动化机器学习实践应用
- 模型动态增量训练
- 模型推理与部署
关联推荐
如果你觉得这篇文章对你有帮助,欢迎通过 微信赞赏码 或者 Buy Me a Coffee 请我喝杯 ☕️